Fourier transform to evaluate the frequency-domain

Question

Question 1:

Use the defining equation for Fourier Transform to evaluate the frequency-domain representations of the following three signals:

a) x(t) = e^-2tu(t -3)

b) x(t) = Σ_m=0^∞ (1/2)^m δ(t-m)

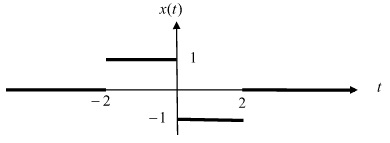
c) x(t) as shown in the figure:

Question 2: 

Use the equation describing the inverse Fourier Transform to determine the time-domain signals corresponding to the following two Fourier Transforms:

a) X(jω) = {cos(2ω), |ω| < π/4
                { 0           otherwise

b) X(jω) = 2jω/3 {u(ω + 3) - u (ω - 3)}

Question 3:

Use the tables of properties of Fourier Transforms and Basic Fourier transform pairs to find Fourier transforms of following three signals:

a) x(t) = sin(2πt)e^-tu(t)

b) x(t) = d/dt (te^-2t sin(t)u(t))

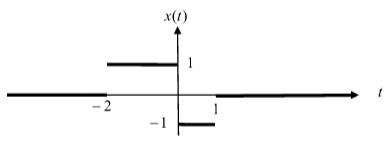
c) x(t) as shown in the figure:

Question 4:

Use the tables of properties of Fourier Transforms and Basic Fourier transform pairs to find inverse Fourier transforms of following two signals:

a) X(jω) = [4sin(2ω - 4)/2ω - 4] - [4sin(2ω + 4)/2ω + 4]

b) X(jω) = [(sin²(3ω)) cosω]/ω²

Question 5:

a) Find the frequency response and impulse response of the system having the output as y(t) and the input as x(t):

x(t) = e^-1ut and y(t) = e^-2t u(t) + e^-3t u(t)

b) Determine the differential equation description for the system H(jω) = (jω - 1)/(ω² + 4). Find impulse response of the system as well.

Question 6:

Consider the system shown in the following block diagram:

Input of the system is z(t) = 2cos(200πt) + 5cos(1000πt). This signal passes through a non-linear device (square) which has output of x(t) = z²t. The signal x(t) is filtered by an ideal band -pass filter which has cut-off frequencies of ω₁ = 6.0π and ω₂ = π

a) Draw the frequency spectrum of z(t), x(t) and y(t).

b) Using the frequency domain representation of y(t), evaluate y(t) in time domain.

c) Replace the ideal band-pass filter with a non-ideal filter to have the same output. Draw the frequency spectrum of this non-ideal filter.