Assignment:
Question 1. Let f(x) be a 2pi- periodic function such that f(x) = x^2 −x for x ∈ [−pi,pi]. Find the Fourier series for f(x).
Question 2. Let f(x) be a 2pi- periodic function such that f(x) = x^2 for x ∈ [−1,1]. Using the complex form, find the Fourier series of the function f(x).
Question 3.
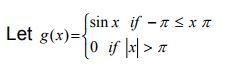
a. Verify that the function g satisfies the condition
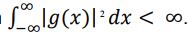
b. Compute the Fourier Integral of g(x).
c. Determine what the Fourier Integral of g(x) converges to at each real
number.
Question 4. Consider the Gaussian function
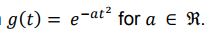
a. Sketch the graph in EXCEL of the Gaussian function when a = −0.1, a = 1 and a = 10 in the same frame.
b. Compute the Fourier Transform of the Gaussian function for a = 1.
Provide complete and step by step solution for the question and show calculations and use formulas.