Lipdon is a company that produces tea bags. Specifically, the company has 5 popular flavors that can be produced at the company's manufacturing plant. The company produces boxes of each flavor and each box contains 25 tea bags. The table below gives the estimated annual demand in boxes and the selling price of a box for each flavor.
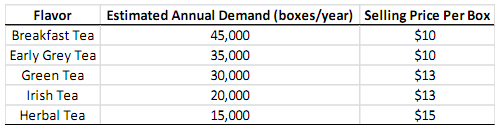
Since Lipdon's manufacturing plant has limited capacity, the company changes the flavors sold each year. As a company policy, if Lipdon decides to produce a flavor for a year, the number of boxes produced of that flavor should be at most the estimated annual demand and at least 90% of the estimated annual demand for boxes of that flavor.
As the production manager at Lipdon, you need to decide on the production plan for the coming year by determining which flavors to produce and how many boxes to produce for each flavor. As noted previously, the company's manufacturing plant has limited capacity. Specifically, 100,000 boxes in total can be produced (production of a box of any flavor uses the same amount of capacity). To be able to produce a flavor, a one-time setup needs to be executed in the manufacturing plant. The table below shows the setup cost associated with each flavor's production as well as the production cost per box for each flavor.
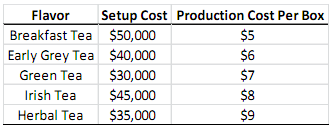
If the setup for a flavor is not executed, boxes of that flavor cannot be produced. As the production manager, you want to find the production plan that will maximize the estimated profits for the coming year. It is assumed that you will sell all of the tea boxes produced and the estimated profit is equal to the revenues gained from sales minus the production costs and the setup costs.
In this problem, you are asked to mathematically formulate a mixed-integer (binary) optimization model for the production planning of tea boxes for Lipdon.
a) Mathematically formulate a mixed integer programming model for the above problem by defining your decision variables, and writing your objective functions and constraints (assume you can produce fractional number of tea boxes).
b) Formulate the following constraints mathematically independent of each other. All of the constraints should be linear.
i. If you produce Breakfast Teas, you cannot produce Irish Teas.
ii. If you produce Irish Teas, you have to produce Herbal Teas.
iii. If you produce Green Teas, you have to produce at least 2 other flavors.
iv. If you produce both Breakfast and Earl Grey Teas, you cannot produce Irish Teas.
v. If 4 or more flavors are produced, Herbal Teas should be one of the flavors produced.