Formulate a network model for problem as a minimum-cost

Question

Question 1a

Consider the transportation problem having the following data.

DESTINATION

	1	2	3	Supply
Source
1	6	7	4	40
2	5	8	6	60
Demand	30	40	30

1. formulate a network model for this problem as a minimum-cost flow problem by drawing a network model.
2. Formulate and solve a spreadsheet model for this problem.

NOTE: using word, insert shapes, lines with arrow draw answer to "a"

Type your name and label drawings.

Using solver and excel for "b" total cost should be $580

Question 1b

The diagram below depicts a system of aqueducts that originate at three rivers (nodes tt, x, and w) and terminate at a major city (node T), where the other nodes are junction points in the system.

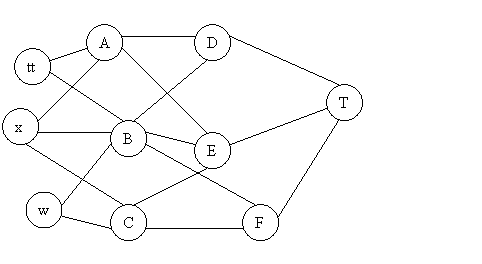
Using units of thousands of acre feet , the following tables show the maximum amount of water that can be pumped through each aqueduct per day.

To/ From	A	B	C
tt	75	65	-
x	40	50	60
w	-	80	70

To/From	D	E	F		To/From
A	60	45	-		D	120
B	70	55	45		E	190
C	-	70	90		F	130

1. formulate this problem as a maximum flow problem by identifying a source, a sink, and transshipment nodes, and then drawing the complete network that shows the capacity of each arc.