Manufacturing Strategy
Suppose that you are the manufacturing strategy developer of a company. Right now, you need to determine where and how to produce a product. Specifically, you need to produce exactly 8,750 units of the product for the next period. There are three plants that you can use for manufacturing the product. Each plant has a fixed payment that you have to pay to use (if you do not pay this fixed payment, you cannot use the plant). The table below shows the fixed payment for each plant.
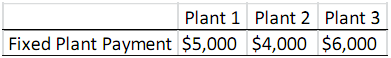
Once you select the plants that you will use for manufacturing, you need to decide how many machines to place in each selected plant. You can place at most 5 machines in each plant (if you do not pay the fixed payment for a plant, you cannot place any machine in that plant). Placing a machine in different plants has different fixed costs. The table below shows the cost of one machine placement in each plant.
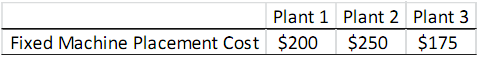
For instance, if you plan to use plant 1, you will pay $5,000 as the fixed plant payment, and you will pay $200 for each machine you place in plant 1. Each machine can produce at most 1,000 units. That is, the machine capacity does not depend on the plant in which the machine is placed (any machine can produce at most 1,000 units wherever it is placed). For instance, if you place 2 machines in plant 3, you can produce at most 2,000 units in plant 3. However, if you decide to use a plant for manufacturing, you have to produce at least 1,500 units in that plant.
Once you know the number of machines in a plant, it is not important how many you produce with each machine in that plant as the production cost per unit is the same for the machines in the same plant. For instance, if you place 3 machines in plant 2, and you decide to produce 2,500 units in plant 2, it does not matter how much of these 2,700 units will be produced with the first, second, or third machines (each can produce 900 or first and second machines produce 1000 while the third machine produces 700) since the unit production cost for each machine within the same plant is the same. However, the unit production cost in each plant is different due to different locations of the plants. The table below shows the production cost per unit produced in each plant.
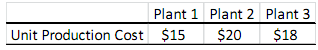
As the manufacturing strategy developer, you need to determine which plants to operate in, how many machines to place in each plant, and how much to produce in each plant so that you can minimize the total costs (plant payments + machine placement costs + production costs) while producing 8,750 units.
Formulate a mixed-integer-linear-programming model for the problem above by defining the decision variables, expressing objective function and constraints as functions of your decision variables and combining everything to get the final formulation.
Note 1: The number of machines placed in a plant should be non-negative integer. The number of units produced in a plant can be fractional.
Note 2: Your model should consist of linear functions only.