For the three vectors in part 11 find the corresponding

Question

Question #1. A matrix A is known as a circular matrix if its 2na row is obtained by circularly shifting the lsi row. Same way 3P¹ row is obtained from rd row and so on. Consider the following 3 x 3 circular matrices A and B:

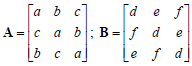
I Show tha C = A B is also a circular matrix.

IL Without computing D, show that D=ABB-B=AB²¹ is also a circular matrix. Justify.

III.Show that the vectors

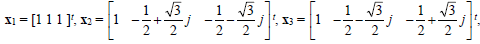
satisfy the linear systems: A x1= λ1x1, Ax2= λ2x2, A x3= λ3x3. Here, j = √-1

IV. For the three vectors in Part 11, find the corresponding values of λ₁, λ₂, and λ₃.

V. Compute the determinant of A.

VI. Create a 3 x 3 matrix X where x₁ is 1^st column, x₂ is 2^nd column & x₃ is 3^rd column.

VII. Compute A^-1 Is A^-1 circular?

VIII.  It is known that we can write A = X A X^-1, where A is a 3 x 3 diagonal matrix having Xi, X2, and A3 on its main diagonal. Using the expression A = X A X^-1, find a matrix E such that A² = X E

IX. Given that first row of a 4 x 4 circular matrix A is [4 3 2 1], write the matrix A.