Flywheels
The aim of this demonstration is to become familiar with the derivation of material indexes in general and for the selection of the optimal material for flywheels in particular.
We willobserve the failure of a flywheel (made of 'blu-tack') and translate the design requirements for a flywheel into material indexes.
Governing Equations
Flywheels store kinetic energy and are finding new application in regenerative braking systems.
We assume the flywheel can be approximated by a disk and so we can write the following for the stored kinetic energy in Joules:
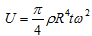(1)
Where r is the density in kg/m3, R is the flywheel radius in m, t is the flywheel thickness in m and w is the angular velocity in radians per second.
The volume of the disk is: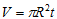 
, so the mass is simply: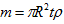 
As the flywheel spins it generates a centrifugal stress, the maximum value of which can be approximated by:
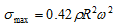(2)
The faster the flywheel spins, the higher the stored kinetic energy and the higher the internal stress. The same holds for density, the more dense the material, the higher the stored energy but also the higher the internal stress. The question is: what is the best material to use for a flywheel?
Questions
1. Convert Equation 2 to an expression in terms of rpm instead of rad/s. Rearrange the equation to give the maximum rpm that can be applied without failure for a material with yield stress sy.
2. Estimate the yielding stress of your blu-tack using a circular cross-section sample and weights/scales. Report three measurements.
3. Assume the density of blu-tack is ~2500 kg/m3 (check this if you have time) and use your equation to estimate the maximum rpm we can expect for a disk of radius R=_____________ mm.
4. Roll out a sheet of blu-tack, punch out a disk with your specified radius, assemble a flywheel for testing on an electric drill and determine the approximate critical rotation speed in rpm. Comment on the outcome.
5. Derive the material index for a light flywheel that stores the most energy per unit mass and that does not yield when spinning. The rotation speed (angular velocity) and geometry do not matter. Identify the constraint, the objective and the free variables. (Hint: establish the energy per unit mass, then eliminate the free variables). Use the relevant chart or the CES software to establish an optimal material - provide a few sentences of explanation.
6. Ignoring the chance of failure and the weight, derive a material index for a flywheel that stores the most energy per unit volume. Use the relevant chart or the CES software to establish an optimal material - provide a few sentences of explanation.