Finding the power spectral density

Question

Response to the following problem:

The information sequence {an}^∞_n= -∞ is a sequence of iid random variables, each taking values +1 and -1 with equal probability. This sequence is to be transmitted at baseband by a biphase coding scheme, described by

         ∞
s(t) = Σ   a_ng(t-nT)
      n=-∞
where g(t) is shown in Figure .

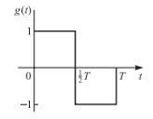
1. Find the power spectral density of s(t).

2. Assume that it is desirable to have a zero in the power spectrum at f = 1/T . To this end, we use a precoding scheme by introducing b_n = a_n + ka_n-1, where k is some constant, and then transmit the {b_n} sequence using the same g(t). Is it possible to choose k to produce a frequency null at f = 1/T ? If yes, what are the appropriate values and the resulting power spectrum?

3. Now assume we want to have zeros at all multiples of f₀ = 1/4T . Is it possible to have these zeros with an appropriate choice of k in the previous part? If not, then what kind of precoding do you suggest to achieve the desired result?