Solve the following problem:
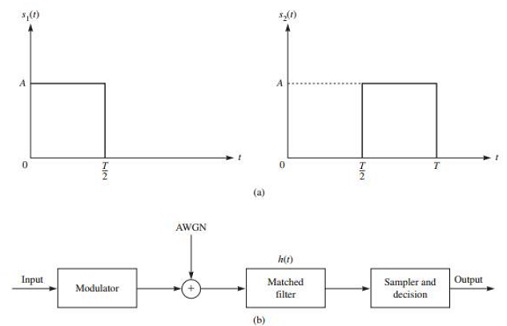
A baseband digital communication system employs the signals shown in Figure (a) for transmission of two equiprobable messages. It is assumed the communication problem studied here is a "one-shot" communication problem; i.e., the above messages are transmitted just once, and no transmission takes place afterward. The channel has no attenuation, and the noise is AWG with power spectral density N0/2 .
1. Find an appropriate orthonormal basis for the representation of the signals.
2. In a block diagram, give the precise specifications of the optimal receiver using matched filters. Label the block diagram carefully.
3. Find the error probability of the optimal receiver.
4. Show that the optimal receiver can be implemented by using just one filter (see block diagram shown in Figure(b)). What are the characteristics of the matched filter and the sampler and decision device?
5. Now assume the channel is not ideal, but has an impulse response of c(t) = δ(t) + ½ δ(t - T/2 ). Using the same matched filter you used in part 4, derive the optimal decision rule.
6. Assuming that the channel impulse response is c(t) = δ(t) + aδ(t - T/2 ), where a is a random variable uniformly distributed on [0, 1], and using the same matched filter, derive the optimal decision rule.