Problem 1. For each of the parts of this question use the information provided to find the consumer’s budget line.
a. Mary optimizes her satisfaction when she consumes 10 books (B) and 5 apples (A) each month. Mary’s monthly income is $50 and she currently spends $10 on apples. Write Mary’s budget line in slope intercept form with books measured on the vertical axis.
b. Joe can consume either 4 pizzas (P) and 10 sodas (S) or 6 pizzas and 1 soda: both of these consumption bundles lie on Joe’s budget line. Write Joe’s budget line in slope intercept form with pizzas measured on the vertical axis.
c. Suzy has $100 in income and she optimizes her satisfaction when she consumes 13 books (B) and 4 (CDs). Suzy only purchases books and CDs. The price of CDs is three times the price of books. Write Suzy’s budget line in slope intercept form with books measured on the vertical axis.
Problem 2. Suppose that you know the utility function for an individual is given by the equation U = XY where U is the total amount of utility the individual gets when they consume good X (X) and good Y (Y). Thus, if U = 10 then the individual can get 10 units of utility from consuming 1 unit of X and 10 units of Y (U = XY = (1)(10)) or from consuming 5 units of X and 2 units of Y or any other combination of X and Y whose product is equal to 10. Given this utility function, the MU from good X is equal to Y (that is, MUx = Y) and the MU from good Y is equal to X (that is, MUy = X). You are also told that this individual’s income is $100 and that the price of good X is $2 and the price of good Y is $4. From this information answer the following set of questions.
a. What is the budget line for this individual given the above information?
b. What is the consumption bundle of good X and good Y that maximizes this individual’s utility given their income, prices of the two goods, and their tastes and preferences as measured by their utility function?
c. Verify the answer you got in part (b) to make sure the individual can afford to buy this consumption bundle.
d. What is the level of utility this individual gets when they maximize their utility given the above information?
Suppose that the price of good X increases to $4 and nothing else changes. Use this new information to answer this next set of questions.
e. What do you predict will happen to the consumption of good X and good Y now that the price of good X has increased?
f. What do you predict will happen to the level of utility this person has relative to the level they had in part (d) now that the price of good X has increased?
g. Find the new consumption bundle that maximizes this individual’s utility now that the price of good x has increased.
h. Verify that the individual can afford the consumption bundle you found in part (g).
i. What is the level of utility this individual has when he maximizes his utility now?
j. Revisit your predictions in parts (e) an d (f). Were your predictions true?
k. Suppose that this individual’s demand for good X is linear. From your work on this problem, find the equation for this individual’s demand curve.
Problem 3. Let’s use the last problem to practice finding the income and substitution effects. In this problem we will be using three different budget lines: BL1, BL2, and BL3. We will also be using two different indifference curves: IC1 and IC2. For this problem assume that the individual’s utility function is still U = XY as it was in problem (2). Also, the MUx = Y and the MUy = X as it was in the last problem.
From problem (2) you found the budget line with income equal to $100, the price of X equal to $2 and the price of Y equal to $4. Let’s call this BL1. In problem (2) you also found the point (let’s call it point A) that maximized this individual’s utility when faced with this level of income and prices and given the individual’s preferences as represented by the utility function (U = XY).
a. Given the values for point A, what is this individual’s level of utility when they consume consumption bundle A?
b. Now construct BL2 using the following information. The individual’s income is still $100, but the price of good X is now $1 and the price of good Y is $4. What is the equation in slope intercept form of this individual’s budget line?
c. Given the information you have about this individual’s utility function and BL2, find the consumption bundle (let’s call this point B) that maximizes this individual’s utility. What is the individual’s level of utility when they consume this consumption bundle?
d. Can this individual afford the bundle you found in part (b)? Does this bundle exhaust this individual’s income?
e. (At this point to guide your work you might want to draw a carefully drafted graph that includes BL1, BL2 and the two bundles that maximize this individual’s utility-bundle A which sits on BL1 and bundle B which sits on BL2. ) Now we want to construct that imaginary budget line, BL3, that is the budget line constructed with the new prices (Px = $1 and Py = $4) and with income adjusted so that the individual returns to their original indifference curve (the curve that point A sits on). Suppose that to have the same level of utility as the individual had at point A, the adjusted income would be $70.72. (Remember that since good X is now cheaper it takes less income to have the same level of utility as the individual had originally.) Given that the level of utility the individual receives when they consume the consumption bundle that maximizes their utility given BL3 must be equal to the level of utility when they maximize their utility with BL1 (consult answer (a) for the amount of this utility), what is the optimal consumption bundle when the individual faces BL3?
f. Verify that the answer you got in part (e) yields the same level of utility as you got in part (a). Verify that the answer you got in part (e) is affordable: that is, does the consumption bundle cost $70.72?
g. The substitution effect with respect to good X is measured by the change in the consumption of good X from point A to point C. Using your calculations from parts (a) through (e) calculate the substitution effect.
h. The income effect with respect to good X is measured by the change in the consumption of good X from point C to point B. Using your calculations from parts (a) through (e) calculate the income effect.
i. Given your work in this problem, is good X a normal or inferior good?
Problem 4. Use the table below that provides a firm’s production and cost data to answer this set of questions. In the table L stands for labor, K stands for capital, Q stands for total output, MPL stands for the marginal product of labor, FC stands for fixed cost, VC stands for variable cost, TC stands for total cost, AFC stands for average fixed cost, AVC stands for average variable cost, ATC stands for average total cost, and MC stands for marginal cost. For this problem assume that the price of labor and the price of capital is constant.
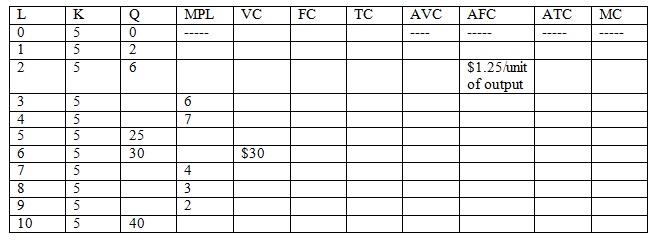
a. Fill in the missing cells in the above table.
b. What is the price of labor?
c. What is the price of capital?
d. At what level of labor usage does diminishing marginal returns to labor first occur?
e. At what level of output is marginal cost equal to average variable cost?
f. At what level of output is marginal cost equal to average total cost? If price is equal to MC is equal to ATC, then what are the firm’s profits? Verify that your answer is correct?
g. If the product sells for $5 per unit in a perfectly competitive industry, how many units should this firm produce? What will the firm’s profits be in the short run?
Problem 5. Suppose a perfectly competitive firm has a total cost function that is equal to TC = q2 + 100q + 100. Furthermore, suppose you know that the firm’s marginal cost function is MC = 2q + 100. From this information answer this set of questions.
a. At what quantity of output is average total cost minimized?
b. What is the value of marginal cost for the output you calculated in part (a)?
c. Suppose that the market demand curve in this market is given by the equation P = 240 – (12/10)Q where P is the price per unit and Q is the total amount of the good produced in the market. Suppose that this perfectly competitive industry is currently in long run equilibrium. How many firms are there in the industry?
d. Suppose that the good in this market is a normal good and that incomes increase. Furthermore suppose the change in income causes the quantity demanded in the market to change by 100 units at every price. Suppose the market supply curve is given by the equation P = (12/10)Q.
i. What will be the new short run price for the market?
ii. How many units of the good will a representative firm produce in the short run given this information?
iii. Calculate the short run profits for a representative firm.
iv. What do you predict will happen in the long run given your answer in part (iii)?
v. What will the long-run price be in this market?
vi. How many firms will there be in the industry in the long run once the market fully adjusts to this change in income?