Finding slope of the line tangent

Question

Assignment:

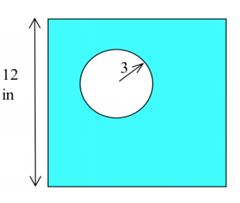
Q1. A circle of radius 3 inches is inside a square with12-inch sides (see figure below). How fast is the area between the circle and square changing if the radius is increasing at 4 inches per minute and the sides are increasing at 2 inches per minute?

Q2. Find dy/dx in two way(a) by differentiating implicitly and (b) by explicitly solving fory and then differentiating. Then find the value of dx/dy at the given point using your results from both the implicit and the explicit differentiation.

x²+5y²=45, point: (5, 2)

Q3. Find dy/dxusing implicit differentiationand then find the slope of the line tangent to the graph of the equation at the given point.
y²-5xy+x²+21=0  point: (2, 5)

Q4. Find dy/dxin two ways: (a) by using the“usual” differentiation patterns and (b) by using logarithmic differentiation.
y=cos⁷?(2x+5)

Q5. Use logarithmic differentiation to Find dy/dx
y=(cos?(x))^x

Provide complete and step by step solution for the question and show calculations and use formulas.