Assignment:
Braess Paradox There are two main roads connecting San Francisco and San Jose, a northern road via Mountain View and a southern road via Cupertino. Travel time on each of the roads depends on the number x of cars using the road per minute, as indicated in the following diagram.
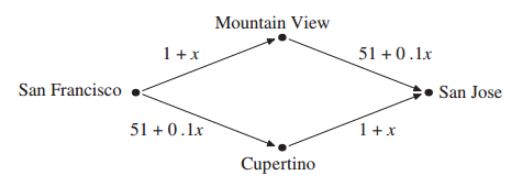
For example, the travel time between San Francisco and Mountain View is 1 + x, where x is the number of cars per minute using the road connecting these cities, and the travel time between Mountain View and San Jose is 51 + 0.1x, where x is the number of cars per minute using the road connecting those two cities. Each driver chooses which road to take in going from San Francisco to San Jose, with the goal of reducing to a minimum the amount of travel time. Early in the morning, 60 cars per minute get on the road from San Francisco to San Jose (where we assume the travellers leave early enough in the morning so that they are the only ones on the road at that hour).
(a) Describe this situation as a strategic-form game, in which each driver chooses the route he will take.
(b) What are all the Nash equilibria of this game? At these equilibria, how much time does the trip take at an early morning hour?
(c) The California Department of Transportation constructs a new road between Mountain View and Cupertino, with travel time between these cities 10 + 0.1x (see the diagram below). This road is one way, enabling travel solely from Mountain View to Cupertino.
Find a Nash equilibrium in the new game. Under this equilibrium how much time does it take to get to San Jose from San Francisco at an early morning hour?
(d) Does the construction of the additional road improve travel time?
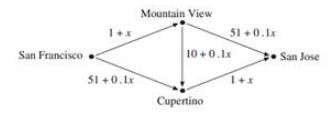
This phenomenon is “paradoxical” because, as you discovered in the answers to (b) and (c), the construction of a new road increases the travel time for all travellers. This is because when the new road is opened, travel along the San Francisco–Mountain View–Cupertino–San Jose route takes less time than along the San Francisco–Mountain View–San Jose route and the San Francisco–Cupertino– San Jose route, causing drivers to take the new route. But that causes the total number of cars along the two routes San Francisco–Mountain View–San Jose and San Francisco–Cupertino–San Jose to increase: travel time along each stretch of road increases. Such a phenomenon was in fact noted in New York (where the closure of a road for construction work had the effect of decreasing travel time) and in Stuttgart (where the opening of a new road increased travel time).
Provide complete and step by step solution for the question and show calculations and use formulas.