Finding local maxima local minima and saddle points

Question

Assignment:

Q1. Find all local maxima, local minima, and saddle points.

1) f(x ,y) = x³ -3x² - 2y² - 9x + 8y + 7
2) f(x ,y) = 9x -xy² + 2y³

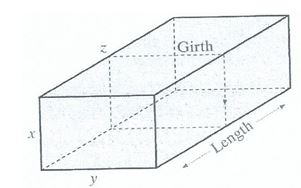
Q2. The postal service has a limit of 108 inches on the combined length and girth of a rectangular package to be send by parcel post. Find the dimensions of the package of maximum volume that can be sent (see drawing).

Q3. Use the method of Lagrange multipliers to find the minimum value of f subject to the given constraint.

1) f(x ,y) = 2x² + y² - 18x -, subject to 3x - y - 8 = 0
2) f(x ,y) = x³ - y³, subject to x - y =10.
3) f(x ,y)  = 6x² - 5xy, subject to 2x - y = 8.
4) f(x ,y) = x²- 4y² + 84xy, subject to 5x +2y = 18.

Q4. Use the method of Lagrange multipliers to find the maximum and minimum values of f subject to the given constraint.

f(x ,y) = 5xy , subject to 9x² + y² = 162.

Q5. Find the equation of the regression line for the given points and (b) draw the scatter diagram and graph the regression line.
(1, 5.2) , (2, 6.4) , (3, 8.1), (4, 9.2), (5,10.6)

Q6. Find the equation of the regression line for the given points
1) (1 , 0.2) (2 , 0.4) , (3, 0.3), (4, 0.6), (5, 0.6)
2) (3.2, 0.10), (4.1, 0.15), (4.8, 0.20) , (5.1, 0.23), (6.0, 0.29)

Q7. Tourism. The total number of foreign tourists visiting the United States, as reported by the U.S Travel and tourism Administration, is shown in the following Table.

Year (x)                            2000        2001      2002      2003       2004
Tourists(y) in millions        25.7        26.3       29.7       34.2         38.3

a) Find the regression line.
b)Estimate the number of foreign tourists that will visit the United States during 2005.

Q8. Evaluate the given double integrals

1) ∫²₀∫³₁ (4-x) dydx

2) ∫¹₀∫²_-1 ye^xy dxdy

Q9. Evaluate the double integrals on the given rectangular region

∫∫^R_R x2√3x + ydA R: -1≤x≤4 and 1≤y≤6

Q10. Evaluate the given double integrals

1) ∫⁴₁∫^x2_x √x/y dydx

2) ∫²₀∫^4-y2₀ y√x dxdy

Provide complete and step by step solution for the question and show calculations and use formulas.