Assignment:
An infinitely long, straight wire carries a constant current I along the z-axis. A rectangular loop of conducting wire (dimensions = a x b) is located in a radical plane at a distance x from the wire, as shown.
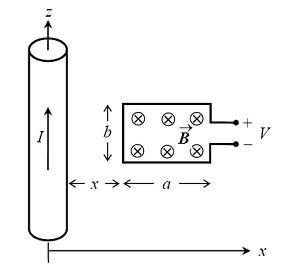
(a) Find the flux of the magnetic-field B through the loop.
(b) If the loop moves in and out in the radial direction such that x(t) is a given function of time, determine the induced voltage V(t).
(c) Show that applying the Lorentz Force Law, F = q(E + V x B), yields the same result as obtained in part (b) based on Faraday's Law.
(d) What happens to the voltage V(t) if x is kept constant, but the loop is moved up and down parallel to the z-axis? Justify your answer by using both Faraday's Law and Loretz's Law.