Assignment:
A binary source has two outputs, a 1 and az, with probabilities 0 .9 and 0 .1.
a. Design Huffman codes for this source and its nth extension (i.e., taking n letters at a time), forn = 2, 3, 4, 5, 6, 7, and find the average codeword length per single source outputs in each case.
b. Plot the average codeword length per single source output found in part (a) as a function of n. On the same plot indicate the entropy of the source.
c. Repeat parts (a) and (b) for a binary source with probabilities 0.6 and 0.4 and notice the difference with the first source.
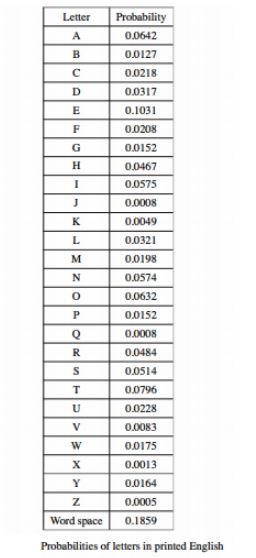
Provide complete and step by step solution for the question and show calculations and use formulas.