Assignment:
Consider a Harsanyi game with incomplete information in which N = {I, II}, TI = {I1, I2}, and TII = {II1, II2}. The mutual beliefs of the types in this game in the interim stage, before actions are chosen, are
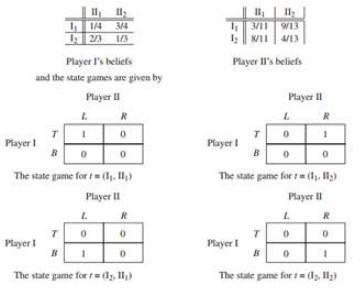
Are the beliefs of the players consistent? In other words, can they be derived from common prior beliefs? If you answer no, justify your answer. If you answer yes, find the common prior, and find a Bayesian equilibrium in the game.
Provide complete and step by step solution for the question and show calculations and use formulas.