Find the slope m of the tangent line to the graph

Question

Assignment:

Determine the values of x, if any, at which the function is discontinuous. At each number where f is discontinuous, state the condition(s) for continuity that are violated.

f(x) {x²+1 if x0
         0  if x=0}

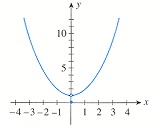
The function f is discontinuous at x=0 because f is not defined at x=0

The function f is discontinuous at x=0 because lim_x→0 f (x) does not exist.

The function f is discontinuous at x=0 because lim_x→0 f (x) exists, but this limit is not equal to f (0).

The function f is continuous everywhere because the three conditions for continuity are satisfied for all values of (x).

Use the Intermediate Value Theorem to find the value of c such that f(c) = M.

f(x)=x2-x+1on[1,8];M=43

Find the slope m of the tangent line to the graph of the function at the given point and determine an equation of the tangent line.

f(x)=7x-3x² at (-1,-10)

Let f(x) = x² + 4x.

f(x) = x² + 4x (a) Find the derivative f 'of f.

(b) Find the point on the graph of f where the tangent line to the curve is horizontal.

Hint: Find the value of x for which f '(x) = 0.

(c) Sketch the graph of f and the tangent line to the curve at the point found in part (b).