A Crosslinked System. Each of the five components in a crosslinked system (shown) is operational in a time interval ?T with the probability of 0.8. The components are independent.
(a) Find the probability that the system is operational during the time period ?T .
(b) If the system was operational during ?T , what is the probability that component E3 had been operational?
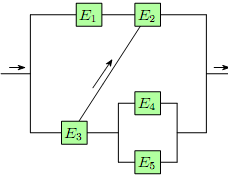
Figure 1: A crosslinked system. If E3 is operational both branches exiting from it are active (think about electricity ?ow). If E3 is not operational neither of the two branches exiting from it is active.
Hint: The problem combines circuits and Bayes' formula. Discuss how the circuit simplifies when component E3 works and, alternatively, when it fails. When E3 works, is E1 relevant? What are the hypotheses needed for the total probability and Bayes' formulae?