Discuss the below:
Q: In recent years, about two-thirds of US house holds purchased ground coffee. Consider the annual ground coffee expenditures for households purchasing ground coffee. Assuming that these expenditures are approximately distributed as a normal random variable with a mean of $65.16 and a standard deviation of $10.00
Using the normal probability:
A. Find the probability that a household spent less than $35.00.
B. Find the probability that a household spent more than $60.00.
C. What proportion of housholds spent between $40.00 and $50.00.
D. 99% of housholds spent less than what amount?
Normal Probability
Mean = 65.16
Standard Deviation = 10
Compute probability: X < 35 ==> 0.13%
Compute probability: X > 60 ==> 69.71%
Compute probability: Range 40 <= X <= 450 ==> 99.41% (i.e., between 2 values)
Find actual score: Percentage ABOVE = 5.00% ==> 81.61 (i.e. % greater than)
Find actual score: Percentage BELOW = 95.00% ==> 81.61 (i.e. % less than)
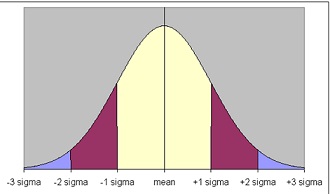
Approximately 68% of all observations within 1 standard deviation of the mean
Approximately 95% of all observations within 2 standard deviations of the mean
Approximately 99.7% of all observations within 3 standard deviations of the mean