Find the normalization conshystant co and the probability

Question

1. Find the order of the group of transformations that leaves an equilateral triangle invariant. Identify the complete set of group elements, find a matrix representation, and then construct the multiplication table. What is the common name of this group?

2. Show that the two expressions below are equivalent.

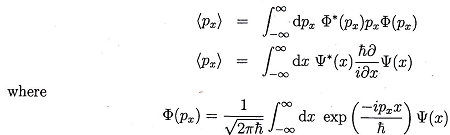
What conditions are necessary for this equivalence?

3. Derive the position-momentum Heisenberg Uncertainty Principle. What is the value of ΔxΔp_x for the Gaussian wave packet

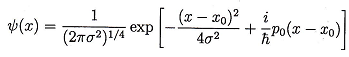
Suppose the variance, cr² is the complex number oi + io-?, then what is the value of axagi_s (be careful about normalization)? What is the solution to the Schrodinger equa­tion of a free particle if 0(x) is taken as the initial condition 0(x, t = 0)?

4. For the wave function, ii)(x) = c_o exp(ip_ox/h)/1/4² + x², find the normalization con­stant c_o and the probability of finding the particle in the interval ±a//5. What is the mean momentum?