PROBLEM #1
Two local flower shops serve a small city. The demand for bouquets of flowers at the first shop depends on both the price of a bouquet at the first shop ( p1 ) and the price of a bouquet at the second shop ( p2 ) as follows: q1 = 136 - 2 p1 + p2 . The demand for bouquets at the second shop is: q2 =136-2p2 + p1. Briefly explain how these demand equations reflect the fact that bouquets at these two flower shops are substitutes.
The first shop has access to a wider network of suppliers, and faces a cost of $10 per bouquet. The cost per bouquet for the second shop, with a small network of suppliers, is $18 per bouquet.
Thus, the cost function for a bouquet of flowers for the first shop is
C(q1 ) = 10q1 , and the cost
function for a bouquet of flowers for the second shop is
C(q2 ) = 18q2 . State the profit function
for each flower shop, with price as the strategic choice variable. Solve for each shop's best- response function. Find the Nash Equilibrium price and quantity for each shop. Compare each shop's choice of price and quantity to the other; briefly comment on your finding.
PROBLEM #2
Two professional soccer teams play each other on a regular basis. One player is about to make a penalty kick. The kicker chooses between kicking the ball left or right at the same time that the goalkeeper decides which way to dive (left or right) to defend the goal. Since the play happens so quickly, each player makes their choice in an effectively simultaneous-move game. The payoffs from choosing where to kick and where to defend are shown below. These payoffs are based on the strengths and weaknesses of the kicker and goalkeeper; both players are fully informed of the payoffs, from having played each other's teams regularly. The payoffs can be thought of as the likelihood of the outcome, following the kick, being in favor of each player; higher values are preferred by both players. The payoffs are listed as (Kicker, Goalkeeper).
Goalkeeper
Drive Left Drive Right
Kicker Kick Left 20, 80 85, 15
Kick Right 75, 25 10, 90
a. Identify all dominant and dominated strategies, if any exist. If none exist, clearly state this.
b. Identify all pure-strategy Nash Equilibria, if any exist. If none exist, clearly state this.
c. Find the mixed-strategy Nash Equilibrium, p and q, where p represents the probability the kicker kicks left and q represents the probability the goalkeeper dives left.
PROBLEM #3
For this problem, consider the sequential-move game below:
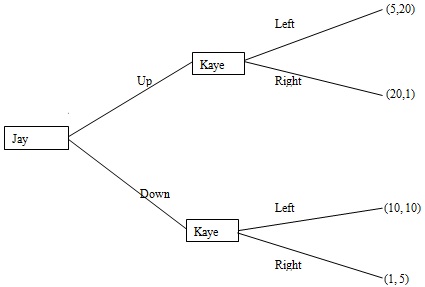
Payoffs: (Jay, Kaye)
a. Identify the pure strategies for each player in this game. Find the rollback equilibrium strategies, using the pruning method to show your derivation.
b. Now represent this sequential-move game using the strategic form. Using cell-by-cell inspection, find all of the Nash Equilibria for this game.
c. Which of your answers in part b is the sub game-perfect equilibrium? Briefly explain why one of the Nash Equilibria in part b would involve strategies that are not credible.
PROBLEM #4
Lyn recently brought his car to Mel's local repair shop for regular maintenance. Shortly after returning home from the shop, Lyn noticed the smell of fuel in his car, which turned out to be caused by a fuel-line leak. Lyn did not have this issue before visiting the shop, and believed that the mechanic must have mistakenly damaged the fuel line during the routine car-maintenance visit. SoLyn called Mel's shop and asked Mel to fix the damage, free of charge. Mel assured Lynthat the car was inspected before it left the shop, and that Lyn must have driven over a sharp object on his way home, after leaving the shop, resulting in the damage. Lyn then considered threatening to cause harm to Mel's reputation by spreading the word to friends and neighbors of the poor quality of Mel's service, if Mel did not repair the damage for free. However, if Lyn did spread negative word of his experience, Lyn's own reputation among his friends could suffer as a result of his complaining and having a negative attitude. Mel's repair shop is low quality with probability p and high quality with probability (1 - p). The basic structure of Lyn's threat is represented below. Payoffs are listed as (Lyn,Mel).
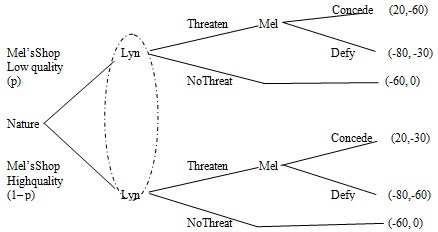
Suppose that Lyn decides to engage in brinkmanship. Lyn tells Mel that if Mel does not concede and pay for the repair, then Lyn will hire an outside expert who, with a probability q, will determine that the fuel line was damaged at the shop, and not while Lyn was driving. If the expert determines that Mel is at fault, Lyn will speak negatively about Mel's shop to friends and neighbors and harm Mel's reputation. If the expert concludes the damage was not Mel's fault, then the payoffs will be those in the "no threat" situation.
a. In the extensive-form representation above, represent the revised payoffs for this game when Lyn engages in brinkmanship.
b. Find the range of values for q for which brinkmanship will be effective. Will brinkmanship be effective for both types of repair shop (high- and low-quality)?
c. Briefly explain what the acceptability condition represents. (You are not required to solve for the condition mathematically; simply state the tradeoff that it represents.)