Question 1: Consider the game:
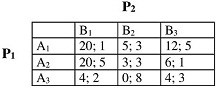
1. List, for each player, the set of all (pure) strategies consistent with rationatizability (When you eliminate any strategy, explain clearly why you eliminate it.)
2 List, for each player, the set of all (pure) strategies remaining after the iterated deletion of weakly dominated strategies.
3 Find all pure-strategy Nash equilibrium and their associated payoffs in this game.
4 Find all mixed-strategy Nash equilibria and their associated payoffs in this game.
Question 2: Consider the game:
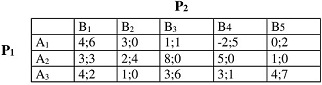
1. List, for each player, he set of all (pure) strategies consistent with rationalizbility (when you eliminate any strategy, explain clearly why you eliminate it.)
2 List, for each player, the set of all (pure) strategies remaining after the iterated deletion of weakly dominated strategies.
3 Find all pure-strategy Nash equilibria and their associated payoffs in this game. 3.4 Find all mixed-strategy Nash equilibria and their associated payoffs in this game.
Question 3: Taxpayers can choose to pay taxes honestly or to cheat. An auditor can choose whether to audit the taxpayers or not. They decide simultaneously. The auditor is very happy not having to audit the taxpayers when they pay taxes honestly. In this case the auditor's utility is 10. The auditor is equally happy if he audits the taxpayers when they cheated. The auditor's utility is 0 if he audits the taxpayers when they are honest. The auditor is very unhappy if he doesn't audit the taxpayers when they cheated. In this case the auditor's utility is -10. If the taxpayers are honest they receive utility of 0. If the taxpayers cheated and they're audited they're going to have to pay a fine 1000 $ and their utility is -20. If they're not audited they get to keep a chunk of money and their utility is 10.
1. Model this situation as a strategic game. Find the Nash equilibrium and its associated payoff in this game. What proportion of the taxpayers cheated on their taxes in the equilibrium?
2. Assume that a government raised a fine for cheating on taxes to 2000 $. If the taxpayers cheated and they're audited their utility is -20. Does the increase of the fine reduce proportion of the taxpayers who cheated on their taxes in the equilibrium? Explain your answer.
Question 4: Consider the game.
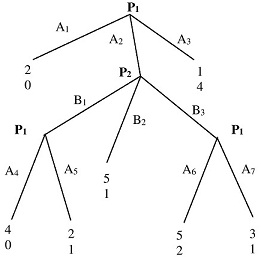
1. Find backward-induction outcome (real actions of the players) of this game. Write the payoffs which players receive at the end of the game.
2. Write down all possible strategies of type A for both players (Note: the set of type A strategies is in general smaller set than the set of type B strategies)
Do so in the following format:
I. a strategy
2. a strategy
3. etc.
Strategies for Player 2:
I. a strategy
2. a strategy
3. etc.
3 Write down all possible strategies of type B for both players.
Do so in the following format:
Strategies for Player 1:
1. a strategy
2. a strategy
3. etc.
Strategies for Player 2:
1. a strategy
2. a strategy
3. etc.
4. Which strategies (of type B) are consistent with backwards induction outcome in this game?
5. Write this game in normal (strategic) form using the strategies of type A.
6. Find all pure-strategy Nash equilibria in this game.
7. List, for each player, the set of all (pure) strategies consistent with rationalizability (When you eliminate any strategy, explain clearly why you eliminate it.)
8. List, for each player, the set of all (pure) strategies remaining after the iterated deletion of weakly dominated strategies.
Question 5: Consider the stage game
|
|
B1
|
B2
|
B3
|
|
A1
|
10;10
|
2;2
|
-2;11
|
|
A2
|
2;2
|
3;3
|
0;0
|
|
A3
|
11;-2
|
0;0
|
5;5
|
1. Find all Nash-equilibria (NE) of the stage game.
2. The stage game is repeated two times with discounting SE (0, 1). Is it possible to support (A1,B1) as a subgame perfect NE in the first round of the repeated game? If it is possible, carefully specify the equilibrium strategy and find the critical discount factor to support this strategy as a subgame-perfect equilibrium. If it is impossible, briefly explain why.
3. The stage game is infinitely repeated discounting 5 e (0, 1). Is it possible to support (A1,B1) on equilibrium path of a subgame perfect NE, yielding (10,10) as the average payoff? If it is possible, carefully specify the equilibrium strategy and find the critical discount factor to support this strategy as a subgame-perfect equilibrium. If it is impossible, briefly explain why.
4. Consider a Stage Game:
|
|
B2
|
B3
|
|
|
B1
|
|
|
A1
|
10;10
|
2;2
|
-2;X
|
|
A2
|
2;2
|
3;3
|
0;0
|
|
A3
|
X;-2
|
0;0
|
5;5
|
What is the highest possible value of X, for which (A1 ;B 1) is played in SPNE for G=(T=2, 6=0,75)? What is the highest possible value of X, for which (Al ;B1) is played in SPNE for G=(T=m, 5=0,75)?
Question 6: Let q1, q2 and q3 denote the quantities of a homogeneous product produced by firms 1, 2 and 3, respectively. Let P(Q) = a - Q be the market-clearing price when the aggregate quantity on the market is Q = q1 +q2 +q3. (More precisely, P(Q) =a-Q for Qa). Assume that there are no fixed costs but firms have asymmetrical constant marginal costs: marginal cost of firm 1 is two times lower than marginal costs of firm 2 and firm 3 (c, = 2c, cz = c3 = c). The firms choose their quantities as follows: firm 1 chooses its quantity first; then, firms 2 and 3 observe qi and simultaneously choose q2 and q3, respectively. What is the subgame-perfect outcome?
Question 7: Consider the game:
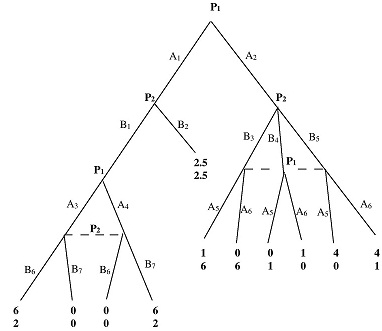
1. State or draw the subgames of this game. How many subgames are in this game?
2. Write down all possible pure strategies of type A for both players (Note: the set of type A strategies is in general smaller not than the set of type B strategies)
Do to in the following format:
Strategies for Player I:
1. a strategy
2. a strategy
3. etc.
Strategies for Player 2:
I. a strategy
2. a strategy
3. etc.
3 Write down all possible pure strategies of type B for both players.
Do so in the following format:
Strategies for Player
I. a strategy
2. a strategy
3. etc.
Strategies for Player 2:
1. a strategy
2. a strategy
3. etc.
4. Find all SPNE of this game. For each SPNE write the payoffs which players receive.
Question 8: Consider the game defined in the following way:
Players 1 and 2 each choose their actions simultaneously. There is a 2/5 probability that payoffs are as in G, and a 3/5 probability that the payoffs are as in Gt. Player 2 knows which game it is. Player 1 does not know it.
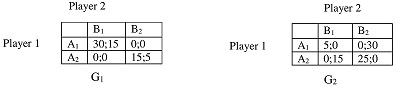
Find all Bayesian Nash Equilibria in the game.
Question 9: Consider the following game. Let q, and qx denote the quantities of a homogeneous product produced by firms 1 and 2, respectively. Let P(Q) = a-Q be the market-clearing price when the aggregate quantity on the market is Q = q, +qx. (More precisely, P(Q) -a-Q for C'ta, and P(Q) = 0 for Q>a). Suppose, that demand is uncertain: it is high (an=50) with probability 0.2 and it is low (at=20) with probability 0.8. Furthermore, the information is asymmetric: firm 1 knows if the demand is high or low but firm 2 does not All of this is common knowledge. Each firm has a marginal cost of c=2 and no fixed costs. The firms choose their quantities simultaneously. What is the Bayesian Nash equilibrium of this game?
It is always advisable to take online assistance from the Game Theory Assignment Help service for making your academic future bright.
Tags: Game Theory Assignment Help, Game Theory Homework Help, Game Theory Coursework, Game Theory Solved Assignments, Bayesian Nash Equilibrium Assignment Help, Bayesian Nash Equilibrium Homework Help