Consider
x = Ax+Bu+Ew
y = Cx,
where
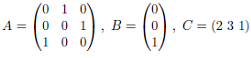
(a) Find the minimum constraint on E such that DDP is solvable.
(b) Find a u = Fr that solves the DDP problem while makes the closed-loop system stable, i.e. A+ BF has only eigenvalues with negative real part.
(c) Verify that there exists an E E V* such that (A, E) is controllable. Explain why even in this case the DDP problem is solvable (namely w(t) will not at all influence the output)