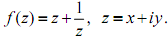Find the inverse transform and find the laplace transform -

Question

Question 1

(a) Using Λf(t)'] = sF(s) - f(0) , show that Λ [sin²(3/2t)] = 9/2s(s² + 9)

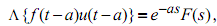
(b) (i) If f(t) has the Laplace transform F(s), then show that

where u(t) is a step function.

(ii) Find the inverse transform of se^-3s/(s² +4)

(c) Find the Laplace transform of f(T) = e^-3t (cost - 3sint). Express it in a simple compact form.

Question 2

(a) Using the Laplace transform method solve the following differential equation:

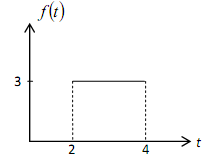
(b) Express the following function in terms of unit step functions and then find its Laplace transform:

(c) Applying the convolution theorem, find h(t) = L^-1{H(s)} for

H(s) = s² /(s² + 4) (s² + 9)

Question 3

(a) Using the technique of Laplace transformation find the solution of the following set of differential equations:

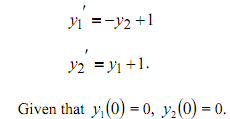
(b) Verify if the function v(x,y) = xy is a harmonic one. If yes then first find its harmonic conjugate u(x,y) and then find the analytic function f(z) = u(x,y) + iv(x+y) as a function of the complex variable z.

(c) Using Cauchy-Riemann equations verify if the following function is analytic: