Find the general solution of the nonhomogeneous

Question

In exercises 1-6, evaluate the integral.

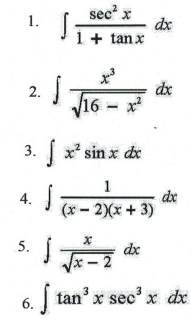
7. Determine whether the improper integral is convergent or divergent. If it converges, find it value.

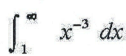
8. Find the length of the curve, y = 2x^3/2, from x = 0 to x = 1

In exercises 9 and 10, determine whether the sequence converges or diverges. If it converges, find the limit.

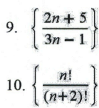
In exercises 11-14, determine whether the series converges or diverges. Indicate the test(s) that you use to support your conclusion.

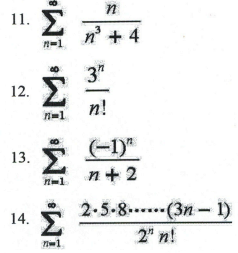
15. Find the values of x for which the series converges. Check endpoints.

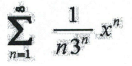
16. Find the first four terms of the Taylor series of f(x) = e^x at a = 1.

17. solve the differential equation.

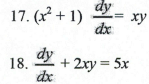
19. Solve the initial-value problem.

y'' + 6y' + 9y = 0 , y(0) = 2 , y'(0) = 1

20. Find the general solution of the nonhomogeneous differential equation, y'' + 3y' - 10y = e^4x

Suggestion: use the method of undetermined coefficients.