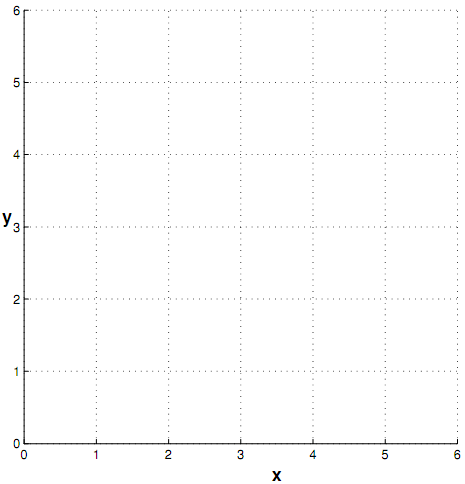
1. This questions is about the differential equation
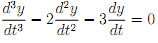
(a) Find the general solution of the differential equation
(b) Write the differential equation as a system of three first order differential equations.
2. Consider the system
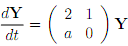
where a is a parameter.
(a) For a = 2:
i. Determine the type of equilibrium at (0; 0), i.e., say whether it is a saddle, spiral sink,etc.
ii. Write down the general solution. Express your answer in terms of real-valued func-tions.
iii. Sketch the phase portrait for the system.
(b) Repeat (a) for a = 3.
(c) Find the type of equilibrium at (0; 0) for all values of the parameter a (i.e. divide a into regions in which the equilibrium is of the same type). Don't forget to include the transitional values.
3. The spread of the chicken pox virus in a population can be modelled by the following system of equations:
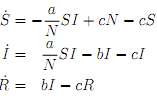
where�
S(t) is the number of susceptible people at time t (that is, the number of people who have not had the disease and who are not immunised),
� I(t) is the number of people infected with the disease at time t,
� R(t) is the number of people who have recovered from the disease (or who are immune) at time t,
� N(t) = S(t) + I(t) + R(t) is the total number of people in the population, and � a, b and c are positive constants.
(a) Show that N does not vary with time in this model.
(b) Briefly explain the physical significance of each term in the model.
(c) The chicken pox vaccine works by making some susceptible people immune to the virus. Briefly explain how you could modify the model to include the effect of vaccinating 90% of all susceptible people.
4. Consider the following system of equations:
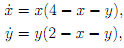
defined for x � 0 and y � 0. A grid is provided on page 3 of this assignment. Use the grid for your answer to parts (b) and (c) of this question. Hand in the grid with your assignment
(a) Find all equilibrium solutions (for x � 0 and y � 0) and determine their types (e.g., spiral source, saddle). For each of the equilibria you find, draw a phase portrait showing the behaviour of solutions near that equilibrium.
(b) Find the nullclines for the system and sketch them on the answer sheet provided. Show the direction of the vector field in the regions between the nullclines and on the nullclines themselves.
(c) Sketch the phase portrait of the system on the answer sheet provided. Your phase portrait should show the behaviour of solutions near the equilibria, and should show a representative selection of other solution curves (i.e., some solutions in each different part of the phase
plane).
(d) Describe the long term behaviour of the solutions through the initial conditions
i. (x; y) = (0; 1)
ii. (x; y) = (2; 2)