Questions:
This is three questions.
Question-1- Find the chromatic number of the graph.
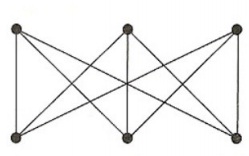
Question 2 - It might be supposed that if a graph has a large number of vertices and each vertex has a large degree, then the chromatic number would have to be large. Show that this conjecture is incorrect by constructing a graph with at least 12 vertices, each of degree at least 3, that is chromatic number 2.
Need Attached Graph in editable format, i.e. xls, doc, etc.
Question #3 - Find the adjacency matrix and adjacency list for the directed graph in the indicated exercise. Order the vertices according to alphabetical order.
Let S - {1,2,4,8} and R = {(1,8), (2,4), (8,2), (4,1), (2,2), (8,1)} be the relation defined S. Draw the directed multigraph of this relation. Need Attached Graph in editable format, i.e. xls, doc, etc.