Module 1 - Introduction to Management Science and Probability
Question 1: The Retread Tire Company recaps tires. The fixed annual cost of the recapping operation is $60,000. The variable cost of recapping a tire is $9. The company charges $25 to recap a tire.
a. For an annual volume of 12,000 tires, determine the total cost, total revenue, and
b. Determine the annual break-even volume for the Retread Tire Company operation profit.
Question 2: Evergreen Fertilizer Company produces fertilizer. The company’s fixed monthly cost is $25,000, and its variable cost per pound of fertilizer is $0.15. Evergreen sells the fertilizer for $0.40 per pound. Determine the monthly break-even volume for the company.
Question 3: The Crumb and Custard Bakery makes coffee cakes and Danish pastries in large pans. The main ingredients are flour and sugar. There are 25 pounds of flour and 16 pounds of sugar available, and the demand for coffee cakes is 5. Five pounds of flour and 2 pounds of sugar are required to make a pan of coffee cakes, and 5 pounds of flour and 4 pounds of sugar are required to make a pan of Danish. A pan of coffee cakes has a profit of $1, and a pan of Danish has a profit of $5. Determine the number of pans of cakes and Danish to produce each day so that profit will be maximized.
a. Formulate a linear programming model for this problem.
b. Solve this model by using graphical analysis
Question 4: In Problem above, how much flour and sugar will be left unused if the optimal numbers of cakes and Danish are baked?
Question 5: The Elixer Drug Company produces a drug from two ingredients. Each ingredient contains the same three antibiotics, in different proportions. One gram of ingredient 1 contributes 3 units, and 1 gram of ingredient 2 contributes 1 unit of antibiotic 1; the drug requires 6 units. At least 4 units of antibiotic 2 are required, and the ingredients contribute 1 unit each per gram. At least 12 units of antibiotic 3 are required; a gram of ingredient 1 contributes 2 units, and a gram of ingredient 2 contributes 6 units. The cost for a gram of ingredient 1 is $80, and the cost for a gram of ingredient 2 is $50. The company wants to formulate a linear programming model to determine the number of grams of each ingredient that must go into the drug in order to meet the antibiotic requirements at the minimum cost.
a. Formulate a linear programming model for this problem.
b. Solve this model by using graphical analysis.
Question 6: A jewelry store makes necklaces and bracelets from gold and platinum. The store has 18 ounces of gold and 20 ounces of platinum. Each necklace requires 3 ounces of gold and 2 ounces of platinum, whereas each bracelet requires 2 ounces of gold and 4 ounces of platinum. The demand for bracelets is no more than four. A necklace earns $300 in profit and a bracelet, $400. The store wants to determine the number of necklaces and bracelets to make in order to maximize profit.
a. Formulate a linear programming model for this problem.
b. Solve this model by using graphical analysis
Question 7: explain the effect on the optimal solution of increasing the profit on a bracelet from $400 to $600. What will be the effect of changing the platinum requirement for a necklace from 2 ounces to 3 ounces?
Module 2: Decision Analysis
Question 1: Solve the model formulated in Problem 7 for Southern Sporting Goods Company graphically.
a. Identify the amount of unused resources (i.e., slack) at each of the graphical extreme points.
b. What would be the effect on the optimal solution if the profit for a basketball changed from $12 to $13? What would be the effect if the profit for a football changed from $16 to $15?
c. What would be the effect on the optimal solution if 500 additional pounds of rubber could be obtained? What would be the effect if 500 additional square feet of leather could be obtained?
Question 2: Rucklehouse Public Relations has been contracted to do a survey following an election primary in New Hampshire. The firm must assign interviewers to conduct the survey by telephone or in person. One person can conduct 80 telephone interviews or 40 personal interviews in a single day. The following criteria have been established by the firm to ensure a representative survey:
o At least 3,000 interviews must be conducted.
o At least 1,000 interviews must be by telephone.
o At least 800 interviews must be personal.
An interviewer conducts only one type of interview each day. The cost is $50 per day for a telephone interviewer and $70 per day for a personal interviewer. The firm wants to know the minimum number of interviewers to hire in order to minimize the total cost of the survey.
Formulate a linear programming model for this problem.
Question 3: Solve the linear programming model formulated in Problem above for Rucklehouse Public Relations graphically.
A. Determine the sensitivity ranges for the daily cost of a telephone interviewer and the number of personal interviews required.
B. Does the firm conduct any more telephone and personal interviews than are required, and if so, how many more?
C. What would be the effect on the optimal solution if the firm was required by the client to increase the number of personal interviews conducted from 800 to a total of 1,200?
Question 4: Describe one example where mathematical modeling can be applied at your workplace. You may consider interviewing a senior officer or a colleague who may have experience in modeling.
Module 3 – Forecasting
Question 1: In the diet example in this chapter, what would be the effect on the optimal solution of increasing the minimum calorie requirement for the breakfast to 500 calories? to 600 calories?
Increase the breakfast calorie requirement to 700 calories and reformulate the model to establish upper limits on the servings of each food item to what you think would be realistic and appetizing. Determine the solution for this reformulated model.
Question 2: Ronald Thump is interested in expanding his firm. After careful consideration, he has determined three areas in which he might invest additional funds: (1) product research and development, (2) manufacturing operations improvements, and (3) advertising and sales promotion. He has $500,000 available for investment in the firm. He can invest in its advertising and sales promotion program every year, and each dollar invested in this manner is expected to yield a return of the amount invested plus 20% yearly. He can invest in manufacturing operations improvements every 2 years, with an expected return of the investment plus 30% (at the end of each 2-year period). An investment in product research and development would be for a 3-year period, with an expected return of the investment plus 50% (at the end of the 3-year period). To diversify the total initial investment, he wishes to include the requirement that at least $30,000 must be invested in the advertising and sales promotion program, at least $40,000 in manufacturing operations improvements, and at least $50,000 in product research and development initially (at the beginning of the first year). Ronald wants to know how much should be invested in each of the three alternatives, during each year of a 4-year period, to maximize the total ending cash value of the initial $500,000 investment.
a. Formulate a linear programming model for this problem.
b. Solve the model by using the computer.
Question 3: Application questions are designed to assist you in applying the tools and techniques covered in each module to the real world environment Interview someone in your crew who is in charge of providing food in your submarine. Does he/she use any model to insure an adequate amount of food for the crew and a balanced diet? How is the cost of each diet computed? Discuss how such a model can be used at your workplace.
Module 4 - Queuing Analysis and Inventory Management
Question 1: Lauren Moore has sold her business for $500,000 and wants to invest in condominium units (which she intends to rent) and land (which she will lease to a farmer). She estimates that she will receive an annual return of $8,000 for each condominium and $6,000 for each acre of land. A condominium unit costs $70,000, and land costs $30,000 per acre. A condominium will cost her $1,000 per unit, an acre of land will cost $2,000 for maintenance and upkeep, and $14,000 has been budgeted for these annual expenses. Lauren wants to know how much to invest in condominiums and land to maximize her annual return.
a. Formulate a mixed integer programming model for this problem.
b. Solve this model by using the computer.
Question 2: Solve the following mixed integer linear programming model by using the computer:
maximize Z = 5x1 + 6x2 + 4x3
subject to 5x1 + 3x2 + 6x3 ≤ 20
x1 + 3x2 ≤ 12
x1,x3 ≥ 0
x2 ≥ 0 and integer
Question 3:
The Texas Consolidated Electronics Company is contemplating a research and development program encompassing eight research projects. The company is constrained from embarking on all projects by the number of available management scientists (40) and the budget available for R&D projects ($300,000). Further, if project 2 is selected, project 5 must also be selected (but not vice versa). Following are the resource requirements and the estimated profit for each project:
Project Expense Management Scientists Estimated Profit
($1,000s) Required ($1,000,000s)
1 $ 60 7 $0.36
2 110 9 0.82
3 53 8 0.29
4 47 4 0.16
5 92 7 0.56
6 85 6 0.61
7 73 8 0.48
8 65 5 0.41
Formulate the integer programming model for this problem and solve it by using the computer.
Question 4:
A transportation problem involves the following costs, supply, and demand:
From To Cost
1 2 3 4 supply
1 $500 $750 $300 $450 12
2 650 800 400 600 17
3 400 700 500 550 11
Demand 10 10 10 10
Solve this problem by using the computer
Question 5: Consider the following transportation problem:
To (cost)
From 1 2 3 Supply
A $6 $9 $100 130
B 12 3 5 70
C 4 8 11 100
Demand 80 110 60
Formulate this problem as a linear programming model and solve it by using the computer.
Question 6: Application questions are designed to assist you in applying the tools and techniques covered in each module to the real world environment. Military maneuvers require complex logistics for buying, storing, and transporting goods. Interview a senior officer in your submarine and describe an example of logistics planning he/she has done for a particular situation.
Module 5 - Project Management
Question 1: The Petroco gasoline distributor in Jackson, Mississippi, supplies service stations in nine other southeastern cities, as shown in the following network
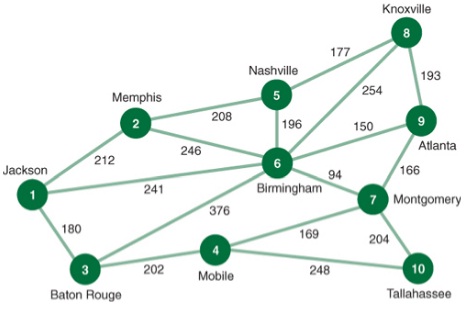
The distance, in miles, is shown on each branch. Determine the shortest route from Jackson to the nine other cities in the network.
Question 2: In 1862, during the second year of the Civil War, General Thomas J. “Stonewall” Jackson fought a brilliant military campaign in the Shenandoah Valley in Virginia. One of his victories was at the Battle of McDowell. Using the following figure and your imagination, determine the shortest path and how long it will take (in days) for General Jackson to move his army from Winchester to McDowell to fight the battle:
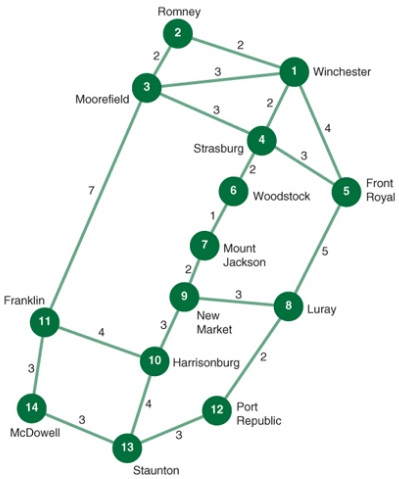
The distance, in miles, is shown on each branch. Determine the shortest route from Jackson to the nine other cities in the network.
Question 3: A new police car costs the Bay City Police Department $26,000. The annual maintenance cost for a car depends on the age of the car at the beginning of the year. (All cars accumulate approximately the same mileage each year.) The maintenance costs increase as a car ages, as shown in the following table:
Car Age (yr.) Annual Maintenance Cost Used Selling Price
0 $ 3,000 $ —
1 4,500 15,000
2 6,000 12,000
3 8,000 8,000
4 11,000 4,000
5 14,000 2,000
6 0
In order to avoid the increasingly high maintenance costs, the police department can sell a car and purchase a new car at the end of any year. The selling price for a car at the end of each year of use is also shown in the table. It is assumed that the price of a new car will increase $500 each year. The department’s objective is to develop a car replacement schedule that will minimize total cost (i.e., the purchase cost of a new car plus maintenance costs minus the money received for selling a used car) during the next 6 years. Develop a car replacement schedule, using the shortest route method.
Question 4: Application questions are designed to assist you in applying the tools and techniques covered in each module to the real world environment. Good project managers are highly sought in business and industry. Describe your experience, if you have worked as a project manager. Alternatively, you can interview someone who may have led a large project in the past.
Module 6 - Linear Programming: Model Formulation, Computer Solutions, and Sensitivity Analysis
Question 1: Construct a Gantt chart for the following set of activities and indicate the project completion time and slack for each activity
Activity Activity Predecessor Time (weeks)
1 — 3
2 — 7
3 1 2
4 2 5
5 2 6
6 4 1
7 5 4
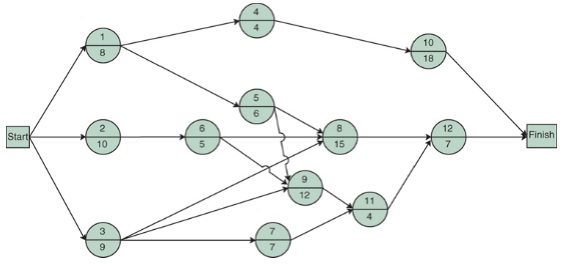
Question 2: Given the following network, with activity times in months, determine the earliest and latest activity times and slack for each activity. Indicate the critical path and the project duration.
Question 3: In one of the little-known battles of the Civil War, General Tecumseh Beauregard lost the Third Battle of Bull Run because his preparations were not complete when the enemy attacked. If the critical path method had been available, the general could have planned better. Suppose that the following planning network, with activity times in days, had been available:
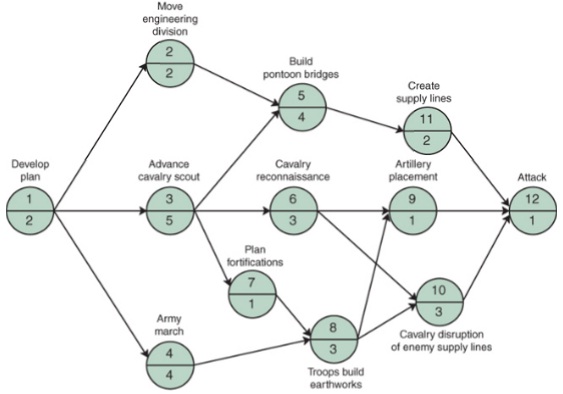
Question 4: Megan Moppett is a sales representative for Technical Software Systems (TSS), and she receives a commission for every new system installation she sells to a client. Her earnings during the past few years have been very high, and she wants to invest in a mutual fund. She is considering three funds: the Temple Global Fund, the Alliance Blue Chip Fund, and the Madison Bond Fund. She has three criteria for selection—potential return (based on historical trends and forecasts), risk, and the fund’s load factor. Megan’s pairwise comparisons for the funds for each of their criteria and her pairwise comparison of the three criteria are as follows:
Return Fund Global Blue Chip Bond
Global 1 1/4 2
Blue Chip 4 1 6
Bond 1/2 1/6 1
Risk Fund Global Blue Chip Bond
Global 1 2 1/3
Blue Chip 1/2 1 1/5
Bond 3 5 1
Load Fund Global Blue Chip Bond
Global 1 1 1/3
Blue Chip 1 1 1/3
Bond 3 3 1
Criterion Return Risk Load
Return 1 3 5
Risk 1/3 1 2
Load 1/5 1/2 1
Determine the fund in which Megan should invest.
Question 5: Alex Wall is shopping for a new four-wheel-drive utility vehicle and has identified three models from which she will choose—an Explorer, a Trooper, and a Passport. She will make her selection based on Consumer Digest ratings, price, and each vehicle’s appearance. Following are Alex’s pairwise comparisons for the vehicles for each of her criteria and her criteria preferences:
Consumer Digest Rating Vehicle Explorer Trooper Passport
Explorer 1 4 3
Trooper 1/4 1 1/2
Passport 1/3 2 1
Price Vehicle Explorer Trooper Passport
Explorer 1 1/4 1/6
Trooper 4 1 2
Passport 6 1/2 1
Appearance Vehicle Explorer Trooper Passport
Explorer 1 4 3
Trooper 1/4 1 1/2
Passport 1/3 2 1
Criterion Consumer Digest Rating Price Appearance
Consumer Digest rating 1 2 4
Price 1/2 1 3
Appearance 1/4 1/3 1
Using AHP, determine which vehicle Alex should purchase
Question 6:
Application questions are designed to assist you in applying the tools and techniques covered in each module to the real world environment
Describe how the tools described in this module can be used to aid you in making decisions in various situations and how you can quickly handle changes in the situation.
Module 7 - Linear Programming Modeling Examples; Transportation and Assignment
Question 1: The Riverwood Paneling Company makes two kinds of wood paneling: Colonial and Western. The company has developed the following nonlinear programming model to determine the optimal number of sheets of Colonial paneling (x1) and Western paneling (x2) to produce to maximize profit, subject to a labor constraint:
maximize Z = $25x1 - 0.8x12 + 30x2 - 1.2x22
subject to x1 + 2x2 = 40 hr
maximize Z = $25x1 - 0.8x21 + 30x2 - 1.2x22
subject to x1 + 2x2 = 40 hr
Determine the optimal solution to this nonlinear programming model.
Question 2:
A metropolitan school system consists of two districts, east and west. The east district contains 35% of all students, and the west district contains the other 65%. A vocational aptitude test was given to all students; 10% of the east district students failed, and 25% of the west district students failed. Given that a student failed the test, what is the posterior probability that the student came from the east district?
Question 3:
The life of an electronic transistor is normally distributed, with a mean of 500 hours and a standard deviation of 80 hours. Determine the probability that a transistor will last for more than 400 hours.
Question 4:
Application questions are designed to assist you in applying the tools and techniques covered in each module to the real world environment.
Discuss with a senior officer at your workplace how the models covered in this module can be applied in planning a route involving multiple intermediate locations. Submit summary of the discussion.
Module 8 - Term Project and Final Exam
Term Project:
The Term Project involves problem analysis, model development, and use of appropriate software to solve a problem. You will submit
(1) a written report on the project using a word processor, (2) a spreadsheet containing the computer solution, and (3) a visual presentation (e.g., PowerPoint) on the project. This presentation should be a business-type presentation summarizing the premises and conclusions of the report with appropriate charts and documentation.
Term Project: Students are required to complete a Term Project that will involve problem analysis, model development, and use of appropriate software to solve the problem. For the project, students will complete the Julia’s Food Booth problem at the end of Chapter 9. Each student will submit (1) a written report on the project, (2) a spreadsheet containing the computer solution, and (3) a visual presentation (e.g., PowerPoint).
Report with Spreadsheet (10% of course grade) You are required to submit a written business report about the assigned exercise. This report is to provide all the details in the problem analysis and solution and provide a permanent, written example of the work you have done to solve the problem for the business. Assume that your pay for the toil you put into this project is dependent on the success of these deliverables. The report should consist of two parts:
1. Microsoft Word document including the material below: Problem statement Discussion of model formulation and the computer solution Evaluation and answers to the questions in the topic (if appropriate)
2. Microsoft Excel spreadsheet file used to solve the model. Presentation (6% of course grade) You are required to prepare a Microsoft PowerPoint presentation of adequate length to explain the problem, solution, and evaluation of the solution (generally, 10-15 slides).
The purpose of the presentation is to explain the problem, solution, and evaluation of your project to your colleagues or senior management. Do not simply repeat the material in the written report or avoid too much detail. Instead, assume this is the key feature of your explanation of what your team has developed to solve the problem. The management team of your contracting business will watch your presentation and use the written report for back-up details as desired. Much of their decision on the project will be based on this presentation and how effectively you sell your solution.
Sample Project To view examples of the required deliverables, click the Resources link in the main course menu. A graphical solution is neither recommended nor acceptable for these problems; you must use an Excel solution.