Find paremetric representations and sketch the path and

Question

Questions

1. Show that f(z) = Re(z) is not differentiable at any z using the limit expression for the derivatives.

2. Are the following functions harmonic? If your answer is yes, find a corresponding analytic function f(z) = u(x, y) + iv(x, y).

(a) u = x² + y²

(b) u = cos(x) cosh(y)

3. Find two sets of paremetric representations and sketch the path.

From (0, 0) to (3, 1) along the axes.

4. By answering the following questions, integrate the function shown below along the given contour.

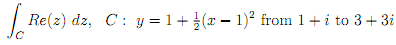
(a) What it the shape of the given contour?

(b) Verify if the integrand is analytic or not.

(c) Evaluate the function.

5. Explain briefly how to verify if Cauchy's integral theorem applies to a function.

6. By answering the following questions, integrate the function shown below along the contour C which is the circle with centre 1 and radius 2 counterclockwise for the

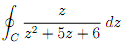
(a) Sketch the given contour C.

(b) Find all singular points (z₀) and indicate them in the same sketch drawn above.

(c) Evaluate the function using Cauchy's integral formula.

7. By answering the following questions, integrate the function below along the unit circle with centre 0 counterclockwise.

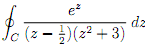
(a) Sketch the given contour and all singular points (z₀).

(b) Using the formula for the derivatives of analytic functions, evaluate the function.

8. Find the Maclaurin series and its radius of convergence of 1/1 + 4iz

9. By answering the following questions, find the Maclaurin series of sin2 z:

(a) Using Eular's equation, express cos(z) using e^iz:

(b) Obtain the Maclaurin series of e^z:

(c) Using the results above, find the series of cos(z): Show the expansion up to 3 terms as well as a general form using ∑.

(d) Express sin²z using cos(2z)

(e) Now find the Maclaurin series of sin²z using the results above. Show the expansion up to 4 terms as well as a general form using ∑.

(f) Obtain the radius of convergence.