Find n for n equal to each of the first ten positive

Question

Part -1:

1. Find n! For n equal to each of the first ten positive integers.

2. Use mathematical induction to prove that x - y is a factor of xⁿ - yⁿ, where x and y are variables.

3. Prove that f_{n - 2} + f_{n + 2} = 3f­_n whenever n is an integer with n ≥ 2. (Recall that f₀ = 0.)

4. Show that if a is an integer, then 3 divides a³ - a

Part -2:

Primes and Greatest Common Divisor

1. Find the smallest prime between n² and (n + 1)² for all positive integers n with n ≤ 10.

2. Let a be a positive integer.  What is the greatest common divisor of a and a²?

3. Use the fact that every prime divisor of

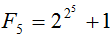                  is of the form 2⁷k + 1 = 128k + 1

to demonstrate that the prime factorization of F₅ is F₅ = 641*6700417.

4. The Indian astronomer and mathematician Mahavira, who lived in the ninth century, posed this puzzle:

A band of 23 weary travelers entered a lush forest where they found 63 piles each containing the same number of plantains and a remaining pile containing seven plantains.  They divided the plantains equally.

How many plantains were in each of the 63 piles? Solve this puzzle.

Attachment:- Final-Exam-for-Chris-Ivy.doc