Find a set of generators for the row space of a and find

Question

1. For the matrices

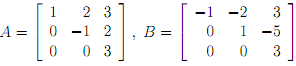
(a) find the eigenvalues and eigenvectors
(b) determine a matrix P so that P^-1 AP = B

2. For the following matrix

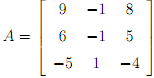
(a) find the eigenvalues
(b) for each eigenvalue determine the eigenvector(s)
(c) determine a matrix P so that B = P^-1 AP is in triangular form, and verify that the determinant of B agrees with what you used in (a)

3. For the following matrix

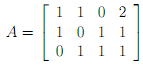
(a) determine the row-rank

(b) find a set of generators for the row space of A

(c) show that any element of the row space of A can be written as a linear combination of your generators.

4. For the following matrix

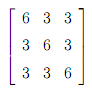
(a) find the eigenvalues

(b) find the eigenvectors corresponding to these eigenvalues

(c) starting with the eigenvectors you found in (a) construct a set of orthonormal vectors (use the Gram-Schmidt procedure).

5. Check whether the set of ordered triples f(2, 0, 2), ( 1, 2, 1), (1, 1, 1)g forms a basis for R³. If so, starting with this basis use the Gram-
Schmidt procedure to construct an orthonormal basis for R³.