Express the listed radical in its minimal expression

Question

Problem 1: Use the prime decomposition of integers to express the listed radical in its minimal expression. Do not use decimals.

a. √(220500)

b. ³√(68600)

c. ³√(3267)√(4400)

d. √(1125)√(2420)

Problem 2: Fill in the table below. Note that you should refer to the section titled "Intervals" on pages 337-338 of the textbook and to Table 1 on page 338.

Interval      Inequality       Representation on the real line

                     x ≤ -1

                                                     °→

                      √3

(-3, Π )

                    3/5 ≤ x

Problem 3: Give the intervals that correspond to the inequalities listed below.

a. All real numbers x so that x ≥ - 2

b. All real numbers x so that 0 < x ≤ 8/3 and x ≤ 2

c. All real numbers x so that x > 3 or -6 ≤ x

Problem 4: In each of the following exercises, rewrite and simplify the given expression. Give your answer using positive exponents only.

a. (5x³yz²/xy²z)^-3/2

b. (uv²w³ - 3u²w)2(v^-2)

c. (√x³ + x²y^-2z)(xy²z³)

Problem 5: In each of the following exercises, expand and simplify.

a. √2(3x - √2x² + 1) - √18(1 - 4x)³

b. (t - u)² + 5(3t - u + 4u²)(1 + u)

c. (1 - 3x + x²)³(2 - 2x²)

Problem 6: In each of the following exercises, factor the given expressions.

a. 2y³ + 6y² + y + 3

b. 3x² - 18xy + 24y²

c. 50x³ + 20x² + 2x

Problem 7: In each of the following exercises, factor and simplify the terms, and then do the indicated operations.

a. 1/9x² - y² - (12x² - 10xy + 2y²)/(9x² - 6xy + y²)

b. √(x² + 5x + 4)/(x² + 8x + 16) - (x² - 3x - 4)/(x² - 16)

c. ((9x³ + 6x² + x)/27 x³ + 1) (6x - 1)/(3x² + x))

Problem 8: Determine which of the equations given below have real solutions and give the solutions of those that do.

a. 2x² + 3x = 6

b. x⁴ + 6x² - 3 = 0

Hint. Set a = x² and express the equation in terms of a.

c. 3x = 12x² - 5x

d. (x² + 7x)/3 = -5/2

e. (3x² + 3)/2 = x

Problem 9:

a. Rationalize the numerator of (√2 -6)/(5 + √2)

b. Rationalize the denominator of (5x - 2)/(√(2+x) -√6x)

c. Rationalize the denominator of (√8xy³ + 5√y)/(2y - √y)

Problem 10: Convert from radians to degrees the numbers given below. Note that you should refer to the section titled "Angles" on pages 358-359 of the textbook.

a. Π/5 + 3Π/8

b. 7Π/4 - √2Π

Problem 11: Convert from degrees to radians for the numbers given below.

a. (38/3)°

b. (90/5)°

Problem 12: Give the exact value of

a. tan (7Π/6)

b. cos (5Π/8) sin(5Π/8)

c. cos2 (Π/8)

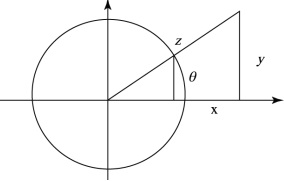
Problem 13: In Unit 1 of the study guide we defined the trigonometric functions using a straight triangle with hypotenuse 1. Use similar triangles to define in any right-angle triangle with hypotenuse z the trigonometric functions as

cosθ = x/z sinθ = y/z tanθ = y/x

Hint. The circle below has radius 1.

Our 24/7 available Prime Decomposition of Integers Assignment Help tutors provides you the opportunity to contact with us anytime and from anywhere, without any problem.

Tags: Prime Decomposition of Integers Assignment Help, Prime Decomposition of Integers Homework Help, Prime Decomposition of Integers Coursework, Prime Decomposition of Integers Solved Assignments, Trigonometric Functions Assignment Help, Trigonometric Functions Homework Help, Trigonometric Functions Coursework, Trigonometric Functions Solved Assignments