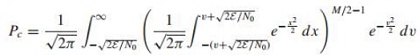Express the error probability in terms of a single integral

Question

Solve the following problem:

Consider a quaternary (M = 4) communication system that transmits, every T seconds, one of four equally probable signals: s₁(t), -s₁(t), s₂(t), -s₂(t). The signals s₁(t) and s₂(t) are orthogonal with equal energy. The additive noise is white Gaussian with zero mean and autocorrelation function R_z(τ ) = N₀/2δ(τ ). The demodulator consists of two filters matched to s₁(t) and s₂(t), and their outputs at the sampling instant are U₁ and U₂. The detector bases its decision on the following rule:

U₁> |U₂|⇒s₁(t)        U₁< -|U₂|⇒ -s₁(t)  

U₂> |U₁|⇒s₂(t)        U₂< -|U₁|⇒ -s₂(t)

Since the signal set is biorthogonal, the error probability is given by (1 - Pc), where Pc is given by Equation . Express this error probability in terms of a single integral, and thus show that the symbol error probability for a biorthogonal signal set with M = 4 is identical to that for four-phase PSK.

Hint: A change in variables from U₁ and U₂ to W₁ = U₁ + U₂ and W₂ = U₁ - U₂ simplifies the problem.

Equation: