Problem 1:
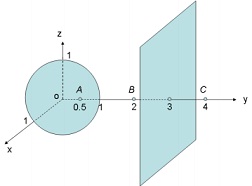
In Fig. 1, the dielectric sphere of radius R0 = 1 m is filled uniformly with charge and the volume charge density is Ρv = 1 mC/m3. Also, the relative permittivity for the sphere is 2. The sheet y =3 m (parallel to x-z plane) is infinite in extent and the surface charge densities Ρs = -1 mC/m2. Figure out the electrical filed intensity at the marked locations A, B and C. (Here are the reference formulae: ds^R = R^R2sinθdθdΦ, and dv = R2sin θdRdθdΦ)
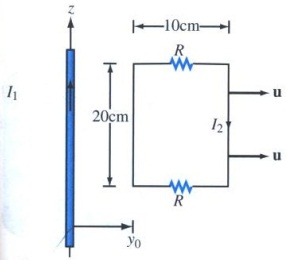
Problem 2: The loop shown in Fig. 2 moves away from a wire carrying a current I1 = 10 cos(2Πt) Ampere at a constant velocity u→= yˆ5 m/s. If R=10 Ω , find I 2 as a function of t. Let's assume that y0=0 at t=0.
Problem 3: An uniform plane EM wave is traveling in the +z direction inside a lossless media with properties μr and εr, and obeys the following equations:
Vector phasor E~(x, y, z) = E~(z) =xˆEx(z)~
∂Ex(z)/∂z2 + k2Ex (z) = 0
1). Express the intrinsic impedance, phase velocity, and the wavelength.
2). Express E~x (z) assuming | E~x (z = 0) | = 0.1 V/m
3). Express H~ (x, y, z)
4). Calculate the instantaneous electrical and magnetic fields assuming μr = 1, εr = 2, initial phase for the electrical field = π, and time frequency = 50 THz (Tera Hz).
5). What are the instantaneous power density and the average power density carried by the wave?
Problem 4: Refer to our textbook
Derive the wave equations of eq. (12.5) starting from the discrete-space models on page 577. This will need to include the explanation of (1) the lumped element discrete-space model in Fig. 12.1, (2) the derivation of the discrete-space equations (12.1) and (12.2), and (3) the detailed derivation of eq. (12.5) from (12.3).
Problem 5: A 1.05 GHz generator circuit with series impedance Zg = 10 Ω and voltage source is vg(t) = 10cos(ωt - 600) (V) is connected to a load with impedance (100+j50) Ω via a 67-cm long lossless transmission line. The phase velocity of the line is 0.7c where c is the speed of light in vacuum. Find the complete solution of d(z, t) and s^(z, t) on the line.