1. Create a market demand schedule from the following data:
At a price of 80 cents per kilogram, the demand for apples is 14,000 kilogram
At 60 cents per kilogram, the demand is 20,000 kilograms
At 40 cents per kilogram, the demand is 26,000 kilograms
At 20 cents per kilogram, the demand is 32,000 kilograms
Graph the demand curve from the given data. Explain why the demand curve slopes downward and to the right, calculate the elasticity of demand and explain.
2. Explain the significance of the co-efficient of the PED calculated in question 1. What exactly does it tell you?
3. If a 6% decrease in the price of peanut butter causes total revenue to increase, what do you know about the demand for peanut butter?
4. If the price of French fries increase from $2.50 dollar to $3.00 dollar and we see that the demand for mayonnaise decreases from 4 units a month to 2 units a month. What do we know about these two goods? Justify your answer.
5. Explain, using demand and supply curves how demand and supply would change for the introduction of a new supermarket into Australia. What might change due to income fluctuations, population trends, consumer expectations and tastes, and advertising. Write your speculations down in an essay format and illustrate with graphs. Include:
a) Market structure
b) Demand/Supply curve of supermarkets and the industry
c) Effects on demand and supply
d) Elasticity of demand and supply
6.
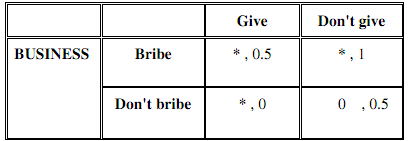
The above game repsesents the interaction between a businessman and a politician. The businessman maximizes profits, and the politician maximizes the probability that he will be re-elected to office.
The businessman wants to persuade the politician to give him a monopoly in a certain industry. If he gets the monopoly, the businessman makes $10 million in profits. He is considering contributing $1 million to the re-election campaign of the politician, to try to persuade her to give him the monopoly. However, this kind of transaction is illegal, so they cannot write a contract on it. Assume that his opportunity cost is zero. As for the politician, the probability that she is reelected if she does nothing is 0.5. If she gives the monopoly to the businessman, this reduces her probability of reelection by 0.5, as she is perceived by the public as being corrupt. If she gets a campaign contribution of $1,000,000, her probability of being re-elected increases by 0.5.
Fill in the payoff matrix, and find any Nash equilibria. Explain what each party should do.