Explain-unique equilibrium levels

Question

Unique Equilibrium Levels : Lead Levels in Blood

Solve the following problem:

1. Unique Equilibrium Levels For any positive values of the input I and the rate constants k_ji show that system (3) has a unique equilibrium solution xi = a, x₂ = b, x₃ = c, where a,b, and c are all positive.

Figure 6.12    Lead transport in the body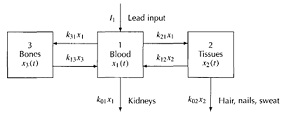

Building the Model ODEs:

Apply the Balance Law to the lead flow through the blood, tissue, and bone compart-ments diagrammed in Figure 6.1.2 to obtain a system of three linear rate equations:

(Blood) x'₁ = -(ko₁ +k₂₁ + k₃₁)x₁ + k₁₂x₂ + k₁₃x₃ +I₁

(Tissues) x'₂ = k₂₁x₁ - (k0₂+ k₁₂)x₂ .......(3)

(Bones) x'₃ = k₃₁x₁ - k₁₃x₃

The intake rate I₁ of lead into the blood from the GI tract and the lungs is a constant or a piecewise continuous function of time.
If I₁ is a constant, then system (3) is autonomous, because the independent variable t does not appear in any rate function. The first thing one does with an autonomous system is to look for constant solutions, i.e., equilibrium solutions. We determine them algebraically by finding values for the state variables that simultaneously make all of the rate functions zero. If I₁ and the coefficients k_ji are positive constants, then system (3) has a unique equilibrium solution x₁ = a, x₂ = b, x₃ = c with a, b, and c all positive. No matter what the initial data or the rate constants k_ji are,the lead levels approach that equilibrium state as t → +∞ .