Solve the following problem:
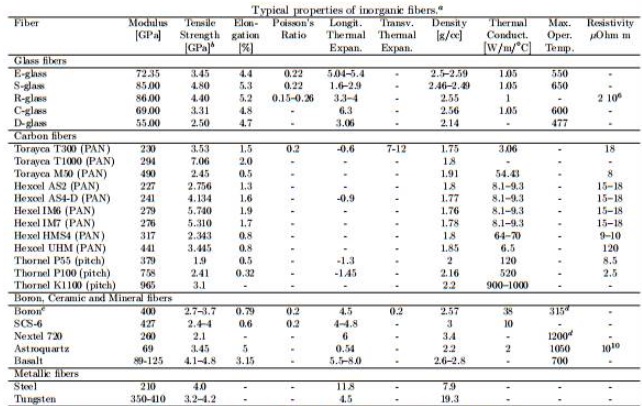
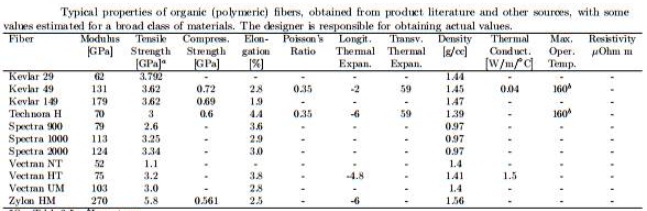
A cylindrical pipe with diameter d = 40 cm is subject to internal pressure p = 20 MP a with a variability given by a COV 20%. The pipe is free to expand along the length so that no axial stress develops in its wall, only hoop stress. The pipe is hoop wound and it is assumed that the fibers carry all the load. Therefore, the stress in the fibers is σf = pd/2tf where tf is the thickness occupied by the fibers only. Assume that a matrix, which does not contribute at all to the strength of the material, occupies a thickness tm = tf. The material properties of the fibers in Tables.
Assume a variability of strength given by a COV of 35% and matrix density ρm = 1.2 g/cc. Designing for a reliability of 99%,
(a) What is the required wall thickness (t = tf +tm) and fiber type that yields the minimum thickness ?
(b) What is the required wall thickness and fiber type for minimum weight?
(c) What is the required wall thickness and fiber type for minimum cost? Use costs in $/kg for the composites given in Exercise 1.
Exercise 1: Define and explain the following terms: strand, end, yarn, and roving.