Explain proof in numerical linear algebra

Question

Questions:

Proof in numerical linear algebra explained in this solution

1. Suppose that C∈C^nxn is invertible and the set S={w1,...,wk} C Cⁿ is linearlyindependent.

    Prove that CS:={Cw1,.. ., Cwk}⊂Cⁿ is linearly independent.

(a) Prove that N(A) = span {V_r+1,...,v_n}, where V₁;...,v_n are the orderedcolumns of V.

(b) Prove that the non-zero singular values of A are equal to the square roots ofthe non-zero eigenvalues of A^HA or AA^H. These last two matrices trave thesame non-zero eigenvalues.

(c) If A∈C^nxn_HER, prove that the sirrgular values are the absoiute values of theeigenvalues of A.

2.Let A∈C^nxn Prove that A is HPD if and only if A = B^HB, where B∈C^nxn is invertible. (Hint for one of the directions, you rlray assume the appropriatefactorization is valid.)

3. LeLµr,s∈C, where n≥r>s≥1, and define L(r,s) = [l^(r,s)_i,j]∈Cnxn via

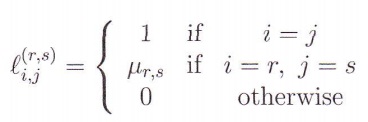
(a) Prove that L^(r1,s)L^(r2,s) = L^(r2,s)L^(r1,s) for any n≥r1>r2>s≥1

(b) Prove or clisprove (using a counter example) that L^(r1,s1)L^(r2,s2) =  L^(r1,s1)L^(r2,s2) for arbitrary indices that satisfy n≥rα>sα≥1,α = 1,2.

(c) Define L(s): =L^(n,s)...L^(s+1,s), for each 1≤s

(d) Write out the matrix L : = (L⁽¹⁾)^-1 ... (L(n^-1))^-1