Discuss the below in detail:
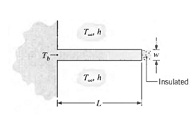
Q: A straight fin of uniform cross section is fabricated from a material of thermal conductivity 50 W/m. K, thickness w = 6 mm, and length L = 48 mm, and is very long in the direction normal to the page. The convection heat transfer coefficient is 500 W/m2 · K with an ambient air temperature of T8 = 30°C. The base of the fin is maintained at Tb = 100°C, while the fin tip is well insulated.
(a) Using a finite-difference method with a space increment of 4 mm, estimate the temperature distribution within the fin. Is the assumption of one-dimensional heat transfer reasonable for this fin?
(b) Estimate the fin heat transfer rate per unit length normal to the page. Compare your result with the one-dimensional, analytical solution,
(c) Using the finite-difference mesh of part (a), compute and plot the fin temperature distribution for values of h = 10, 100, 500, and 1000 W/m2 · K. Determine and plot the fin heat transfer rate as a function of h.