Assignment:
Diagram shows M at position x with spring force -kx acting to accelerate the mass toward the origin. Note that this is a spring which exerts force to the left for positive x and to the right for negative x. This means that net force and acceleration are always toward the center origin of the motion.
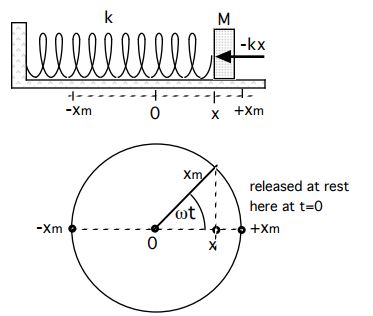
SHM parameters shown on a reference circle. Here, the moving point is at position x moving toward origin with negative velocity, and also with negative acceleration (toward center).
On a frictionless table, mass M is attached to the free end of a spring whose force constant is k. The free end is located at the origin of an x axis. The other end of the spring is fixed. Now the mass is moved toward +x to position the free end at xm, and at that point is released from rest.
PART A.
Apply the second law, 'net force = ma' to the moving mass at position x. Expressing the acceleration a as the second derivative of x, write an equation (1) in terms of only parameters k, M, and x. (HINT: This equation is a second order differential equation. One solution for it is of the form (2) x= A cos (omega t) in which constants A, and (omega) must be found in terms of given parameters k and M.
PART B.
Take the first and second derivatives of (2), and use them to eliminate A and t to express (omega) in terms of k and M. From (2) identify the constant A.
Finally, write (4) x(t), and (5) v(t), and (6) a(t) in terms of k, M, xm, and omega.
Use the above to write (7) a(x) and (8) v(x).
PART C.
Given constants are: k= 36 nt/m, xm= .25 m, and M= 1.44 kg. Substitute these givens into general equations (4) to (8) to calculate the following:
The period T; position x, velocity v, and acceleration a, all at t= .30 sec.;
Position x when v= - .8 m/sec; acceleration a when x= -.10 m; time t when x= -.12 m.