Equation of a circle with the indicated center and radius

Question

Discuss the below:

Q1: Determine symmetry with respect to the x axis,y axis,or origin.If any exists and graph

y=x/2 +1

y=2x

|y|=-x

y=-x

Q2: Find the distance between the indicated pairs:

(-6,4),(2,-1)

Q3: Write the equation of a circle with the indicated center and radius

C(0,0),r=6

C(-1,-3),r=√5

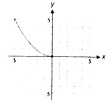
Q4: The fig show a portion of a graph.Extend the given graph to one that exhibits the indicated type of symmetry

(a)x asis only

(b)y asis only

(c) origin only

(d) x and y axes

 

Q5: Find the equation of the line with the indiacted slope and y intercept.Write down the final answer in standard form Ax+By=C, A>=0

Slope=-1;y intercept=7

Slope=5/3,y intercept=6

Q6: Find the equation of the line passing through the given point with the given slope.Write the final answer in slope intercept form y=mx+b

(4,0);m=3

Q7: Find the equation of the line passing through the two given points.Write the final answer in slope intercept form y=mx+b or in the form x=c

(-1,4);(3,2)

Q8: Write an equation of a line that contains the indiacted point and meets the indicated condition(s).Write the final answer in the standard form Ax+By=C. A>=0

(-3,2);parallel to y=4x-5

(-1,3);perpendicular to y=-3x/5 +2

Q9: Indicated whether each set defines a function.Find the domain and range of each function.

{(-1,4),(0,3),(1,2),(2,1)}

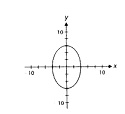
Q10: Indicated whether each graph is a graph of function

Q11: Determine which of the equation define a function with depende4nt variable x.For those that do.find the domain.For those that do not,find a value of x to which there corresponds more than one value of y

3x²+y³=8

x³+|y|=6

k(s)=√-1-s

g(t)=³√5-t

g(x)=4√x-x²

f(x)=5-3x²