Question 1.
a. Suppose you are given the following two points that sit on a straight line:
(x, y) = (10, 2) and (5, 4)
What is the equation for this line in slope - intercept form? Show all your work in finding this equation.
b. Suppose you are asked to find the equation in slope - intercept form of a straight line that has slope = 4 and contains the point (100, 50). Find this e quation, showing all the work you did.
c. You are given the two equations:
y = 4x + 20
y = 100 – x
Find the (x, y) coordinate values where these two lines intersect each other. Show your work. d. You are given the equation: y = 10 – 2x for y ≤ 10 Draw a sketch of this line for all values of x and y that are ≥ 0. Label this line 1. Now, suppose that for every y value, the x value doubles. Draw this new line in your graph showing just the values of x and y that are ≥0. Label this line 2. Write an equation for line 2 showing your work.
e. You are given the equation: y = 10 – 2x for y ≤ 10 and told that for every x value in this original equation, the y value has increased by 10 units. Draw a graph that illustrates the original line as well as this new line. Label these two lines Line 1 and Line 2, respectively.
Then, write the equation for Line 2 and provide a verbal explanation for how you found this new equation.
Question 2. More math review:
a. Joe is taking math this semester and on the first day of class his instructor informed the class that grades would be determined by their scores on three midterms and a final. Each midterm would be worth 20% of their final numeric grade while the final would be worth 40% of their final numeric grade. Joe is try ing to figure out what score he needs on his final in order to accumulate a final numeric score of 90 on a 100 point scale. Complicating Joe’s analysis is that the three midterms have not been on a 100 point scale nor will the final exam be on a 100 point scale, yet the assignment of the final numeric grade will be on a 100 point scale. This is the information that Joe has:
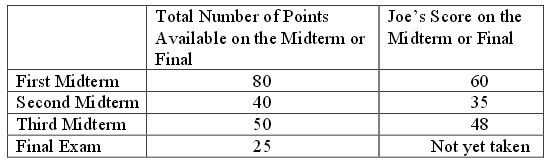
i. Recalculate Joe’s scores for each midterm based on a 100 point scale for each exam (i.e. express Joe’s scores as a score out of 100). Show your work.
ii. Calculate what score Joe must make on the final exam, measured on a 100 point scale, in order to have a final numeric grade of 90 for the class. Show your work.
iii. Recall that the final exam is actually a 25 point exam, so convert Joe’s score on a 100 point final exam to the equivalent score on a 25 point final exam. Show your work. Round to the nearest whole number.
Question 3. Susie and Joe produce two goods: brownies (B) and pies (P). Susie and Joe have the same amount of resou rces available to them. If Susie uses all of her resources to produce brownies she can produce 20 brownies and if she uses all of her resources to produce pies she can produce 10 pies; and if Joe uses all of his resources to produce brownies he can produce 40 brownies and if he uses of his resources to produce pies he can produce 30 pies. Assume that both Susie and Joe have linear production possibility frontiers.
a. Draw a graph that represents Susie’s production possibility frontier given the above info rmation. Measure brownies on the vertical axis and pies on the horizontal axis.
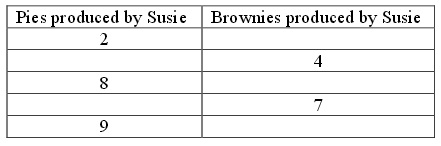
b. Write an equation for Susie’s production possibility frontier given the above information. Write this equation in slope intercept form. Then fill in the following table using this equation.
c. Draw a graph that represents Joe’s production possibility frontier given the above information. Measure brownies on the vertical axis and pies on the horizontal axis.
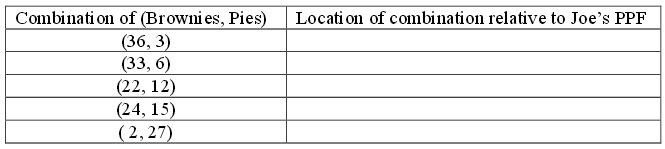
d. Write an equation for Joe’s production possibility frontier given the above information. Determine for each of the following combinations of (brownies, pies) whether the combination lies on Joe’s PPF, lies inside Joe’s PPF, or lies be yond Joe’s PPF.
e. Given the above information, who has the absolute advantage in the production of brownies? Explain your answer.
f. Given the above information, who has the comparative advantage in the production of brownies? Explain your answer.
g. Draw Susie and J oe’s joint PPF. Measure brownies on the vertical axis and pies on the horizontal axis. Identify any intercepts as well as the coordinates for any “kink” points. Write an equation in slope intercept form for every segment of this joint PPF and provide the r elevant range for each segment.
h. What is the acceptable range of trading prices in terms of pies for 10 brownies? Illustrate this using the number line approach presented in class. Make sure to include the arrows and labels that indicate Joe’s perspect ive and Susie’s perspective.
i. What is the acceptable range of trading prices in terms of brownies for 5 pies? Illustrate this using the number line approach presented in class. Make sure to include the arrows and labels that indicate Joe’s perspective and Susie’s perspective.
Question 4. Jacob and Marley produce windows and doors using only their labor. The following table provides you with information about the amount of labor that Jacob and Marley must use in order to produce these doors and windows. Assume that Jacob and Marley both have the same amount of labor and that their PPFs are linear.

a. Given the above information, who has the absolute advantage in the production of windows? Explain your answer.
b. Given the above information, who has the absolute advantage in the production of doors? Explain your answer.
c. Given the above informatio n, what is Jacob’s opportunity cost of producing one window? Explain your answer.
d. Given the above information, what is Marley’s opportunity cost of producing three doors? Explain your answer.
e. If Jacob and Marley each have 120 hours of labor, what combination of (doors, windows) represents each of these individuals completely specializing in their comparative advantage? Explain your answer