Assignment 1:
Q.1 (a) The expression
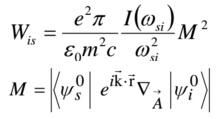
gives, in the usual notation, the transition probability per unit time for a transition between states i and s in the presence of an EM wave. Give the steps and arguments that show how this eventually leads, in the electric dipole (ED) approximation, to the result
(b) Develop the treatment to show how selection rules arise in the ED approximation.
(c) Explain what is meant by the parity of a state function and argue that an electric dipole transition can only take place between states of opposite parity.
(d) An assembly of identical atoms is in equilibrium with blackbody radiation. At what temperature does the rate of induced emission equal the rate of spontaneous emission for a transition of wavelength 589.6 nm?
Q.2 Answer all parts:
(a) Give a brief account of longitudinal and transverse modes in a laser, and indicate what techniques are used to control the wavelength and mode content in the output.
(b) Explain (i) the Q-switching of the laser output in certain laser systems, and (ii) what determines the pulse width obtained when the longitudinal modes of a laser are locked in phase to produce ultrashort pulses.
(c) In the case of the lowest-order transverse mode (Gaussian or TEM00 mode), write down expressions for the beam radius w and the radius of curvature of the beam R, in terms of the radius w0 of the beam at the beam waist, and the distance z from the point of minimum beam-waist.
(d) Show that R can be expressed as R = z + zR2/Z, and explain the significance of zR.
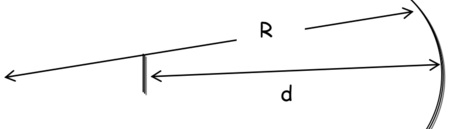
(e) Calculate zR for the cavity of length d, consisting of one plane mirror and one spherical mirror of curvature R, if R = 100 cm and d = 76 cm. Calculate also the beam waist diameter, the spot size on the plane mirrors, and the beam divergence. The wavelength of operation is 632.8 nm.
Q.3 Answer all parts.
(a) Give an account of the rotational and vibrational energy levels of diatomic molecules. Explain how these energy levels affect the spectra of such molecules in the microwave and infrared spectral regions, indicating the origin of the transitions in each region. In your answer, distinguish between heteronuclear and homonuclear molecules and explain the selection rules that govern the transitions observed.
(b) Given the bond length of the 12C16O molecule is 1.128 x 10-12 m, calculate
(i) the energy (in cm-1) of the lowest rotational transition in absorption for this molecule, and
(ii) the resolution needed to separate this transition from that of 13C16O.
(c) Show that the rotational quantum number, Jmax , corresponding to the most intense line in the absorption spectrum is Jmax ≈ 0.59 √[T(K)/B(cm-1) and the energy shift of the band maximum from the band origin is given by ΔE ≈ 1.18√BT
Q. 4 (a) Given the expression,
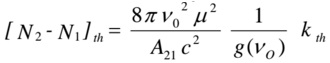
in the usual notation, for the population inversion required at threshold in a laser, derive an expression for the current density required at threshold in a homo-junction diode laser. Explain clearly any simplifying assumptions you make.
(b) Explain how the poor carrier and optical confinement in homojunction lasers was substantially improved by changes to the diode laser physical construction.
(c) A GaAlAs diode laser has a 400 μm cavity length and an effective absorption (loss) coefficient of 800 m-1. The refractive index of the laser is 3.5 and the end faces of the laser are uncoated crystal facets. Calculate the optical gain coefficient at the lasing threshold and the longitudinal mode spacing, in nm, for this laser, which operates at 850 nm.
(d) Briefly outline the advantages of lasers as light sources for spectroscopy.
Q.5 Answer TWO of the following, at least one from section A.
Section A:
(a) Sketch in a qualitative manner the energy level diagrams for the sodium and helium atoms and give clear physical arguments to explain their general form.
(b) Explain what is meant by spin-orbit coupling and show that it adds a term of the form AL.S to the Hamiltonian, where A is a constant. Show that, with the addition of this perturbation, total angular momentum J is still a good quantum number. Calculate the splitting of the 3P term in helium in terms of the constant A.
Section B:
(c) Discuss briefly the principal line-broadening mechanisms of optical transitions in a gas discharge. Derive the line-shape function for Doppler-broadening of an electronic transition in a gas discharge and use it to calculate the Doppler width of the transition at 632.8 nm in a Neon discharge at 400 K.
(d) List the different techniques used to modulate optical beams. Describe in more detail how acousto-optic effects can be used for optical modulation and describe two different regimes of acousto-optic modulation.
Assignment 2:
Q.1 Answer all parts.
(a) Describe how light matter interactions differ for nanostructures compared to bulk materials.
(b) Derive an expression for the exponential attenuation of light in bulk materials, given by
I = (1 - R)Ioe-αl
where I0 is the intensity of light incident on the material, R is the reflectivity, α is the absorption coefficient, and l is the thickness of the sample. Show how this equation can be adapted so that it can be used to describe optical absorption by nanoparticles suspended in a solution.
(c) Estimate the absorption cross section, at λ = 405nm, for a CdS nanowire which is 14 nm in diameter and 1 μm in length and which is suspended in a toluene solution (εm = 2.2). The dielectric and refractive index properties of CdS are given by εs= 6.72+i 2.31, ns = 2.63 and ks = 0.44 (at 3.0eV). Assume that the field enhancement factor is given by f(ω) = 2[2εm/(εm+εs(ω))]
Explain the origin of the field enhancement factor.
Q.2 Answer all parts.
a) Describe the dimensionality of the confinement and how this impacts the states available for electrons and holes in semiconductor quantum wells, quantum wires and quantum dots.
b) Derive the following expression for the spatial form of the wavefunction,
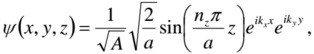
associated with a particle in a potential energy field, V(x,y,z), given by
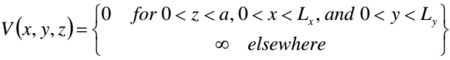
All the terms have their usual meanings.
c) Describe how selection rules for inter-band transitions between a hole and electron in such a structure can be predicted by the overlap integral. Comment on what determines which transitions will be most likely.
Q.3 Answer all parts.
a) Compare and contrast the energy dependence of the number of states available for a single particle to occupy when confined in a quantum well, a quantum wire, and a spherical quantum dot.
b) Estimate the number of states present per unit energy in a microscopic 1μm CdTe cube. Assume the effective electron mass me = 0.1mo and the electron energy of interest is 100 meV above the bulk conduction band edge. Express your result in units of eV-1
c) Use quantitative arguments to predict the level of confinement, if any, experienced by the electrons or holes in the microscopic CdTe structure described above. (mh = 0.35m0, ε = 10.9)
Q.4 Answer all parts.
(a) Compare the number of surface to bulk atoms in a spherical nanoparticle, of radius 6 nm, of a material formed with a ZnS structure where the length of the unit cell is 0.41 nm.
(b) Draw a simple labelled apparatus for organometallic preparation of quantum dots. Describe how this apparatus can be used to synthesise CdSe quantum dots.
(c) Describe how quantum dots could be used as molecular beacons for identifying the presence of specific biological components.
Q.5 Answer all parts.
a) Briefly compare and contrast scanning tunnelling microscopy and electron microscopy for sizing nanostructures on surfaces.
b) Describe in detail how the deflection of the cantilever in an atomic force microscope is determined. Discuss the different modes of operation and the sensitivity of the technique in your answer.
c) Derive a simple formula to estimate the cantilever sensitivity. Estimate the displacement of the cantilever where the cantilever of length l = 1μm, encounters an object of height a = 1nm, when the distance from the cantilever to the detector, L=1cm, and the angle of incidence of the laser on the cantilever is θ = 60o.
Assignment 3:
Q.1 Answer all parts.
(a) Compare and contrast the characteristic length scales associated with the electronic properties of metallic and semiconductor nanoparticles. Comment on at what length scale size effects will arise in each case.
(b) The root mean square distance diffused by an adsorbed atom, in a time t, in one direction on the surface of a crystalline material is given by
(4Dsurfacet)1/2
where Dsurface isthe coefficient of surface diffusion. Fully interpret this equation and discuss what typical process parameters can be adjusted to optimise the distance travelled by adsorbed species prior to immobilisation on surfaces.
(c) Estimate the energy of a particle confined to the three lowest energy levels in a spherical quantum dot. Write down the functional form of the probability density in the radial direction associated with the lowest energy state.
(d) Estimate the alloy fraction, x, of Indium to Gallium in InxGa1-xAs, to produce a 1% compressive strain in an InxGa1-xAs epilayer on a GaAs substrate. Assume that the lattice constant for GaAs and InAs are 5.65A and 6.05A, respectively. Identify what limitations apply to the growth of thick strained epitaxial layers.
Q.2 Answer all parts.
a) Show that the energy for a particle, described by the following spatial form of the wavefunction,
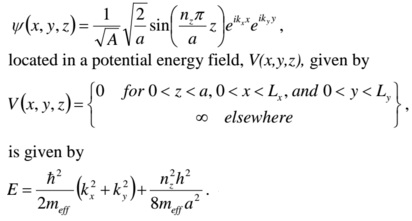
All terms have their usual meanings.
b) Using reasonable values, design an infinite quantum well device which, when an electron recombines with a hole via an intra-band transition, results in a visible photon of light being emitted. Identify, using selection rules, what other photon energies may be emitted from the same device.
c) If the electron and hole described in part (b) form an exciton prior to recombination, discuss the different levels of confinement which can take place and comment on how this will impact upon the precise energy of the photon emitted from excitonic recombination in the quantum well.
Q.3 Answer all parts.
(e) At low temperatures CdSe can have a zinc blende (sphalerite) structure with a lattice constant of 0.608nm. Using this structure, estimate an approximate ratio of surface to volume atoms for a nanoparticle with a diameter of 7 nm.
(f) Describe the process of arrested precipitation and Ostwald ripening used in the organometallic fabrication of CdSe quantum dots. Draw a labelled schematic of the apparatus in your answer. Also describe typical steps taken to prevent agglomeration of particles during or after growth.
(g) Discuss the principal motivation for core quantum dots fabricated with a surrounding shell. Speculate how these might be fabricated using the techniques described in part (b). Give an example structure to support your answer.
Q.4 Answer all parts.
a) Briefly describe the principle of scanning tunnelling microscopy and how it can be applied to determine the morphology of surfaces.
b) If the wavefunctions for the electron, with an energy E, in scanning tunnelling tip, barrier, and metallic sample are given by respectively, show that the tunnelling current is given by Ψ1(x) = Aeikx + Be-ikx, Ψ2(x) = Ceβx + De-βx and Ψ3(x) = Eeikx , respectively, show that the tunnelling current is given by
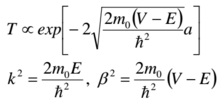
V is the energy of the barrier and is large compared to the energy of the electron in the tip and sample, and a is the distance between the tip and the material.
c) Assuming a barrier height of V = 3eV and the energy of the electron in the tip to be E = 1eV, confirm the phenomenal sensitivity of the scanning tunnelling microscope by estimating the change in current when the distance between the tip and the substrate is reduced by 0.5 nm due to surface roughness. Assume the rest mass of the electron applies throughout and that the Fermi energies of the tip and sample are equal.
Assignment 4:
Q.1 Answer all parts.
(a) Briefly explain what is meant by blazed gratings and holographic gratings. Estimate the linear dispersion (in nm/mm) of a Czerny-Turner grating spectrometer of 1.0 m focal length, fitted with a grating of 1200 grooves/mm.
(b) Explain what is meant by the parity of a wavefunction and explain why electric dipole transitions can only take place between states of opposite parity.
(c) The beam waist in a hemispherical-cavity gas laser, of length 1.2 m, is 1 mm in diameter and is located close to the plane output mirror. The wavelength of operation is 488 nm. Estimate (i) the radius of curvature of the curved output mirror so that it will match the curvature of the laser beam at the mirror, (ii) the diameter of the laser beam at the distance of 10 m from the laser output mirror, and (iii) the beam divergence.
(d) Explain what is meant by spatial coherence and temporal coherence of a laser beam. Calculate the coherence lengths of a He-Ne laser with a resonator length of 30 cm which is oscillating in 3 longitudinal modes.
Q.2 Answer all parts.
(a) Give an account of the rotational and vibrational energy levels of diatomic molecules. Indicate the transition selection rules that apply and explain why homonuclear diatomic molecules are transparent throughout the microwave and infrared spectral regions. Explain any simplifying assumptions.
(b) A term bx3 must be added to the harmonic oscillator potential to more accurately describe the interatomic potential in a diatomic molecule. Discuss the qualitative effects will this have on the wavefunctions and on the energy levels and on the selection rules for vibrational transitions.
(c) Four consecutive lines of the 63Cu1H rotational spectra were measured as shown the table below.
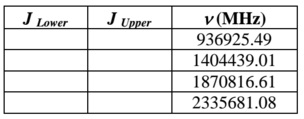
(i) Determine the rotational constant (in cm−1 to 2 significant figures).
(ii) Approximately what would the rotational constant be for 63Cu2D?
(iii) Label the J numbers of the transitions.
Q.3 (a) In the case of one of the laser types given below, describe its operation with as much quantitative detail as possible. Discuss (i) the energy level structure in the active medium, (ii) the method used to obtain population inversion, (iii) the spectral characteristics of the output. State whether the output can be Q-switched or spectrally tuned.
(i) CO2 laser (ii) He-Ne laser
(iii) Semiconductor diode laser (iv) Nd-YAG or ruby laser
(b) The concentration N of Cr3+ ionsin a ruby rod, 10 cm long and 10 mm in diameter, is 1.6 x 1019 cm−3. Give a brief physical argument to justify the expression
Pth = (N/2)EP/τrad
for the minimum pumping power Pth required at threshold, where EP is the mean photon energy required to reach the pump bands (2.6 eV) and τrad is the radiative lifetime of the upper lasing level (3 ms). Assuming 25% of the electrical energy delivered to the flash-lamp is converted into light and that only 20% of this light falls within useful absorption bands, estimate the minimum electrical power to be supplied to reach threshold. Explain why approximately 50% of the Cr3+ ions must be excited in order to reach threshold.
(c) For the 632.8 nm line in neon, A21 = 5x106 s-1 and the Doppler width of the transition under operating conditions is 1500 MHz. The laser cavity mirrors have reflectivities of 100% and 98% at this wavelength. Estimate the population inversion/unit volume required to achieve threshold of oscillation at the centre of the 632.8 nm line in a laser having L = 0.30 m.
Q.4 Answer TWO of the following, at least one from section A.
Section A:
(a) Sketch the energy level diagram of He and give physical arguments to account for the positions of the lowest excited energy levels. Indicate briefly how the energy level picture will be changed for elements later in the periodic table with outer electron configurations similar to He (two s electrons). Calculate the splitting of the 3Po under the spin-orbit interaction − λL.S.
(b) Give a brief account of Raman spectroscopy and describe a typical experimental setup. By considering the possible vibrational modes of the CO2 molecule, explain clearly why they are not all Raman-active and not all active in infrared absorption. List some of the advantages of Raman over infrared absorption spectroscopy.
Section B:
(c) Explain the techniques of Q-switching and mode-locking of lasers and explain clearly how it is normally achieved. Explain how the results obtained depend on the characteristics of the laser media. A Nd:glass laser is 0.8 m long. Assuming that there are 800 participating longitudinal modes, calculate the round trip time and the expected pulse duration when mode-locked.
(d) List the important characteristics of laser sources, compared to classical sources, which make them useful in a range of applications. Set up the energy balance equation that governs the use of a CW laser in laser cutting and discuss briefly the thermo-physical properties of a material which are important in laser materials processing.