Assignment:
Q1. Fill in the fourth column of the Table - the probability of tumor, which is the number of rats with tumors divided by the number of rats in the sample
Table: Hypothetical Data for Kil-EZ Carcinogenicity Test
Number of test rats
|
Number of rats with tumors
|
Rat test dose in mg Kil-EZ per kg rat body weight (mg/kg/day)
|
Probability of a rat's developing tumors
|
Lower 95% confidence level
|
Upper 95% confidence level
|
|
50
|
1
|
0
|
.02
|
|
|
|
50
|
5
|
20
|
.10
|
|
|
|
50
|
10
|
40
|
.20
|
|
|
|
50
|
20
|
80
|
.40
|
|
|
|
50
|
7*
|
160
|
.14
|
|
|
Q2. Explain why the probability is lower at a dose of 160 mg/kg.day than at a dose of 80 mg/kg.day
Q3. Plot the points on a graph with probability on the vertical axis (y-axis) and dose on the horizontal axis (x-axis).
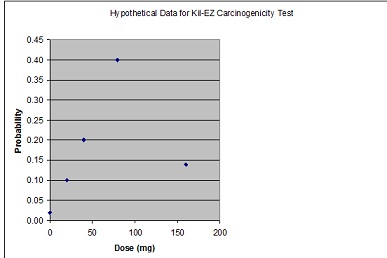
Q4. Draw a straight line through your points to the origin (x = 0, y = 0) and calculate its slope the way you did in high school algebra. That is the cancer potency in kg-day/mg.(If you don't remember how to calculate the slope of a straight line, ask) Should you include the observed probabilities of tumor at the zero dose and the highest dose? Why or why not?
Q5. Using equation, calculate the dose that would correspond to cancer probabilities of 1E-6 and 1E-4. (That is the range EPA considers in setting regulatory standards.)
Now suppose that many different scientists repeated the same experiment. Would they all get exactly the same answers? Probably not. Even though the rats are specially bred, one set of rats is not likely to be exactly the same as another with respect to their reaction to the pesticide. How might the answers differ? Here the statisticians get into the act. They define something they call a standard deviation (s) and they tell us that:s = square root [p*(1-p)/n]
where p is the measured probability that you just inserted into the fourth column of the Table, and n is the number of animals in the test at that dose level. The statisticians also tell us that if the experiment were repeated many times:
* 99% of the results would fall in the range form (p - 2.57s) to (p + 2.57s)
* 95% of the results would fall in the range from (p - 1.96s) to (p + 1.96s)
* 90% of the results would fall in the range from (p - 1.64s) to (p + 1.64s)
The "ranges" are referred to respectively as the 99% confidence interval (sometimes called confidence level), the 95% confidence interval, and the 90% confidence interval. The EPA typically uses the 95% confidence interval in setting standards. Note that at the 95% confidence level, 2.5% of the measured probabilities are expected to be higher than (p 1.96s) and 2.5% of the measured probabilities are expected to be lower than (p - 1.96s).This analysis is based on the normal distribution curve.
With that as background, let's continue with our example.
Q6. Calculate the 95% confindence intervals for each of the relevant probabilities in your Table, and insert into the fifth and sixth columns of the Table.
Number of test rats
|
Number of rats with tumors
|
Rat test dose in mg Kil-EZ per kg rat body weight (mg/kg/day)
|
Probability of a rat's developing tumors
|
Lower 95% confidence level
|
Upper 95% confidence level
|
|
50
|
1
|
0
|
.02
|
0.0000
|
0.0588
|
|
50
|
5
|
20
|
.10
|
0.0168
|
0.1832
|
|
50
|
10
|
40
|
.20
|
0.0891
|
0.3109
|
|
50
|
20
|
80
|
.40
|
0.2642
|
0.5358
|
|
50
|
7*
|
160
|
.14
|
0.0438
|
0.2362
|
Q7. Using the uppper 95% confidence level for the 20 mg/kg-day dose, calculate the cancer potency by drawing a straight line from the 20 mg/kg-day dose level to the origin.
Q8. Do the same using the lower 95% confidence level.
Q9. Calculate the range of doses that would corrrespond to a one in a million risk (p = 1E-6) using your answers to Questions 7 and 8.
Q10. What conclusions do you draw from your answer?
Q11. If you were the EPA administrator, would you ban Kil-EZ to avoid human cancers? Explain your answer.