Problem: In the classic characterization of the prisoner's dilemma, two hypothetical suspects, Ken Lay and Andy Fastnow, are arrested by the FBI. Assume the FBI has insufficient evidence for a conviction, and having separated both prisoners, visit each of them and offer the same deal: if one agrees to confess and implicates the other, while the other remains silent, the silent accomplice receives the full 10-year sentence and the confessor gets 1 year. If both stay silent, the FBI can only gain a conviction on a lesser charge for which both prisoners will get 2 years in prison. If both confess, they will each receive a 5-year sentence. Each prisoner has two options: to remain quiet and not implicate the accomplice, or to betray the accomplice and confess. The outcome of each choice depends on the choice of the accomplice. However, neither prisoner knows the choice of the accomplice. Assume both prisoners are completely selfish and their only goal is to minimize their own jail terms.
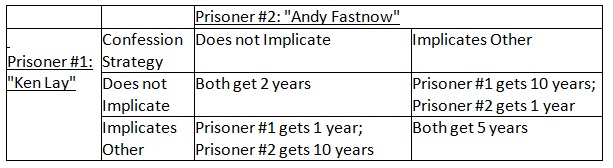
A. Is there a dominant strategy in the classic prisoner's dilemma problem?
B. Illustrate how the classic prisoner's dilemma problem shows that independent rational behavior can sometimes lead to a suboptimal outcome for everybody.