Discuss the manufacturing a spherical pressure vessel

Question

Assignment:

Problem 1.  You are hardening a steel surface by carburization at 1,000 °C using a hydrocarbon gas. (a) Suppose you know that the carbon concentration drops from 5 at.% at 1 mm depth to 4 at.% at 2 mm depth. Estimate the flux of C atoms in this region. (b) Next, suppose that you are given that the hydrocarbon gas establishes a surface concentration of Cs = 1.0 wt.% C and that the initial, uniform  composition of your metal is C0 = 0.2 wt.% C. How long will it take your steel to reach a composition 0.6 wt.% C at a depth of 1 mm? Data: ρFe = 7.63 g/cm3 at 1,000 °C, D0 = 2.0 × 10-5 m2/s, Q = 142 kJ/mol. Hint: You will need a way to calculate erf-1(z), i.e., a table or calculator.

Problem 2. You have the following materials available for manufacturing a spherical pressure vessel:

Alloy	[MPa]	P[g/cm3]	Price[$/kg]
1040 plain-carbon steel	600	7.80	0.63
304 stainless steel	205	7.80	3.70
3003-H14 aluminium	145	2.73	3.00
Ti-5AI-2.5s	827	4.46	15.00

If the stress σ in the (thin) wall of spherical vessel pressurized to pressure p is given by

ó= P^R/ 2t

where t is the thickness of the vessel wall and R is its radius. Calculate the mass of a vessel constructed so that the stress in the wall is less than the yield stress, including a safety factor of Which material gives the lightest vessel? Which material gives the cheapest? Hint: for a thinwalled pressure vessel in which t is small, t² and t³ are ≈ 0.

Problem 3. The function

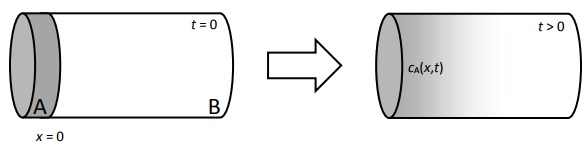
c_A(x,t) = b/ √πD_At ^exp [-x²/4D_At]

describes the concentration c (in atom fraction) after diffusion of A in a cylinder of material B which has had a disk of material A welded to one of its ends (see diagram). At what depth x in the cylinder of B does the concentration of A reach 0.1% after time t = 1,000 s at 1,000 K? Data:

D0 = 10-¹⁰ m²/s, b = 10,000 m, and Q = 20,000 J/mol.

Problem 4.  The critical shear stress for dislocation motion τc is a physical parameter that depends on a number of different structural variables, such as the dislocation density ρ.

This relationship is sometimes summarized as τ_c(ρ) = τ₀ + A√ρ ,

where τ₀ and A are constants. From experiments performed on copper, τ_c = 0.69 MPa for ρ = 10⁴ mm^-2 and τ_c = 2.0 MPa for ρ = 10⁵ mm^-2. What is the yield stress σy of single crystal of copper when ρ = 10⁶ mm^-2 and the crystal is loaded along an axis that makes an angle of φ = 65° with the slip plane? (Take the slip direction angle to be λ = 45°.)

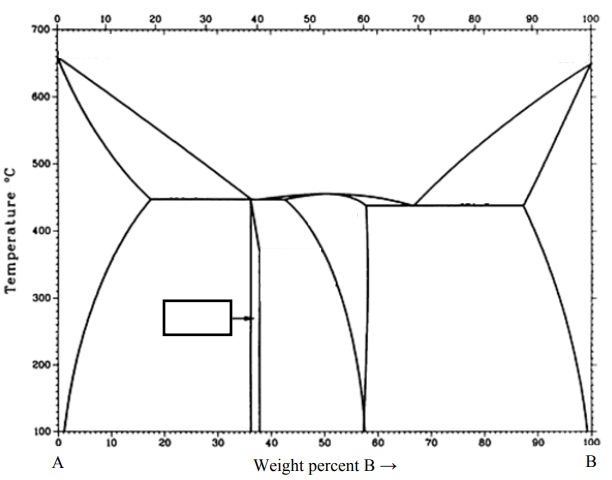
Problem 5.  Label the various phases in this phase diagram (L, α, β, etc.)

Problem 6.  A sample of brass was deformed in a tensile test, producing the following data. The initial length of the specimen was l0 = 35 mm and the initial area was A0 = 10.5 mm2. What are the (a) elastic modulus, (b) the 0.2% offset yield stress, and (c) the ultimate tensile stress. What are the true stress and true strain at the point of highest load? Making a plot of these data could help.

Load [N]                 Extension[mm]

0                                  0.0000

66                                0.0112

177                              0.0157

327                              0.0199

462                              0.0240

797                              1.72

1350                            5.55

1720                            8.15

2220                             13.07

2690                            22.77

2410                            25.25

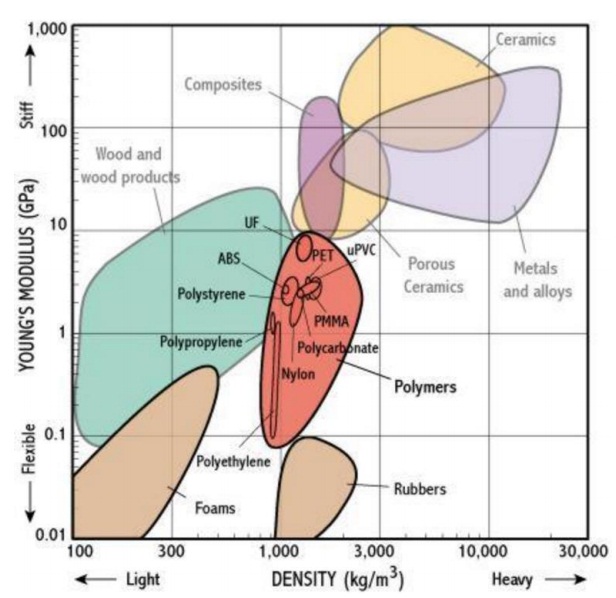
Problem 7.  Suppose that you are designing a component that has a volume of 50 cm³. If the total mass of the component is to be no more than 60 g and the elastic modulus must be at least 2.0 GPa, what polymers can be used to fabricate the part?