Assignment:
The one-dimensional, time-dependent Schrodinger equation is
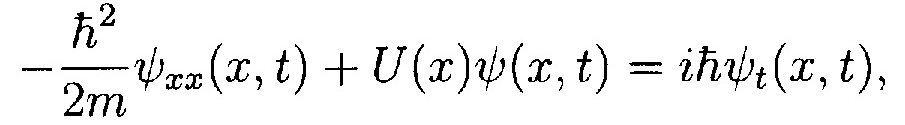
Where ψ(x, t) is the wavefunction for a particle, m is the mass of the particle, U(x) is the potential energy, and h is Planck's constant divided by 27. (The i in the equation is i = √-1. ) In this problem, we'll use -oo < x < oo, t > 0 as our domain.
a) In the case of a free particle, we take U(x) ≡ 0. Use a Fourier transform to solve Schroclinger's equation assuming that ψ(x, 0) = ƒ(x). You don't have to perform the inverse Fourier transform. You may leave your answer for ψ(x, t) in the form of an integral.
b) Suppose that U(x) = I1 (x) = {1 if |x| < 1.
{0 if |x| > 1.
For those interested, this potential would describe a particle outside a finite-wall box, and ψ(x, t) would be the solution to a scattering problem.) Apply the Fourier transform to Schrodinger's equation to show that ψ(k, t) = F[ψ(x, t)) satisfies an integro-differential equation. You don't have to solve that equation.