Discuss the below:
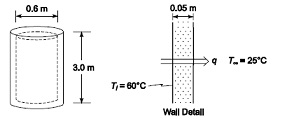
Q: A homeowner wants to replace an electric hot-water heater. There are two models in the store. The inexpensive model costs $280 and has no insulation between the inner and outer walls. Due to natural convection, the space between the inner and outer walls has an effective conductivity of 3 times that of air. The more expensive model costs $310 and has fiberglass insulation in the gap between the walls. Both models are 3.0 m tall and have a cylindrical shape with an inner wall diameter of 0.60 m and a 5 cm gap. The surrounding air is at 25°C, and the convective heat transfer coefficient on the outside is 15 W/(m2 K). The hot water inside the tank results in an inside wall temperature of 60°C.
If energy costs 6 cents per kilowatt-hour, estimate how long it will take to pay back the extra investment in the more expensive hot-water heater. State your assumptions.
GIVEN
Two hot-water heaters
Height (H) = 3.0 m
Inner wall diameter (Di) = 0.60 m
Gap between walls (L) = 0.05 m
Water heater #1
Cost = $280.00
Insulation: none
Effective Conductivity between wall (keff) = 3(ka)
Water heater #2
Cost = $310.00
Insulation: Fiberglass
Surrounding air temperature (T?^?) = 25°C
Convective heat transfer coefficient (hc) = 15 W/(m2 K)
Inside wall temperature (Twi) = 60°C
Energy cost = $0.06/kWh
ASSUMPTIONS
Since the diameter is large compared to the wall thickness, one-dimensional heat transfer is assumed
To simplify the analysis, we will assume there is no water drawn from the heater, therefore the inside wall is always at 60°C
Steady state conditionsprevail