Discuss the behavior of the displacement xt for c2 positive

Question

Aging Spring and Bessel Functions

A model for a mass-spring sys­tem with an aging spring. Without damping, the displacement x(t) at time t is governed by the equation

 mx''(t) + ke^-ηtx(s) = 0,

where m, k, and η are positive constants. The general solution to this equation can be expressed using Bessel functions.

The coefficient of x suggests a change of variables of the form s = αe^βt. Show that transforms into

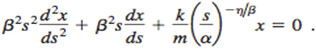
(b) Show that choosing a and 13 to satisfy

η/β = 2 and k/mβ²α^-η/β = 1

transforms (10) into the Bessel equation of order 0 in s and x.

(c) Using the result of part (b). show that a general solution to (9) is given by

x(t) = c₁J₀(2/η√k/me^-ηt/2) + c₂Y₀(2/η√k/me^-ηt/2) ,

where J_o and Y_o are the Bessel functions of order 0 of the first and second kind, respectively.

(d) Discuss the behavior of the displacement x(t) for c₂ positive, negative, and zero.

(e) Compare the behavior of the displacement x(t) for t a small positive number and η a large positive number.