Let {X1(t), t≥0} and {X2(t), t≥0} be independent two-state continuous-time Markov Chains on the states 0 and 1 having the same generator matrix.
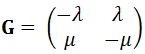
Define Y(t)= X1 (t)+ X2 (t)at any time t
Argue that {Y(t), t≥0} is a continuous-time Markov Chain on the states {0,1,2} and determine its generator matrix.